Home » Subject » Logic
Importance: Low ✭
Author(s): Graham, Ronald L.
Subject: Logic
Keywords: Goodstein Sequence
Recomm. for undergrads: no
Prize: $25 Graham
Posted by: mdevos
on: October 7th, 2008
Question   How many steps does it take the sixth Goodstein sequence to terminate?

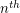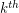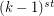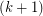For a positive integer $ n $, the $ n^{th} $ Goodstein Sequence is defined as follows. The first term of the sequence in $ n $. To obtain the $ k^{th} $ term, write the $ (k-1)^{st} $ term in hereditary base k notation, change all $ k $'s to $ (k+1) $'s and then subtract 1. If the sequence hits 0, then it terminates. So, the first terms of the sixth Goodstein Sequence are as follows:

\[ \begin{array}{lll} \mbox{term} & \mbox{value} <br> 1 & 2^2 + 2 = 6<br> 2 & 3^3 + 2 = 29<br> 3 & 4^4 + 1 = 257 <br> 4 & 5^5 = 3125 <br> 5 & 5 \cdot 6^5 + 5 \cdot 6^5 + 5 \cdot 6^4 + 5 \cdot 6^3 + 5 \cdot 6^2 + 5 \cdot 6 + 5 = 46655 \end{array} \]

Surprisingly, despite the fact that Goodstein Sequences grow quite quickly at the start, all such sequences do eventually hit 0 and terminate. This result, first discovered by Goodstein, is of interest in logic since it cannot be proved in Peano arithmetic.

Although determining particular properties of a specific Goodstein Sequence are of limited mathematical value, this problem is an interesting computational challenge.

Bibliography



* indicates original appearance(s) of problem.
5 comments

Reply

Comments are limited to a maximum of 1000 characters.
More information about formatting options