login/create account
Problem Given two codes 
, their Tensor Product 
is the code that consists of the matrices whose rows are codewords of 
and whose columns are codewords of 
. The product is said to be robust if whenever a matrix 
is far from , the rows (columns) of are far from (, respectively).
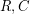, their Tensor Product 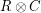is the code that consists of the matrices whose rows are codewords of 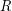and whose columns are codewords of 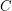. The product 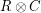is said to be robust if whenever a matrix 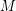is far from 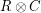, the rows (columns) of 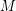are far from 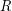(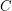, respectively).
The problem is to give a characterization of the pairs 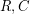whose tensor product is robust.
The question is studied in the context of Locally Testable Codes.
Bibliography
*[BS] Eli Ben-Sasson, Madhu Sudan, Robust locally testable codes and products of codes, APPROX-RANDOM 2004, pp. 286-297 (See ECCC TR04-046).
[CR] D. Coppersmith and A. Rudra, On the robust testability of tensor products of codes, ECCC TR07-061.
[DSW] Irit Dinur, Madhu Sudan and Avi Wigderson, Robust local testability of tensor products of LDPC codes, APPROX-RANDOM 2006, pp. 304-315 (See ECCC TR06-118).
[GM] Oded Goldreich, Or Meir, The Tensor Product of Two Good Codes Is Not Necessarily Robustly Testable, ECCC TR07-062.
[M] Or Meir, On the Rectangle Method in proofs of Robustness of Tensor Products, ECCC TR07-061.
[V] Paul Valiant, The Tensor Product of Two Codes Is Not Necessarily Robustly Testable, APPROX-RANDOM 2005, pp. 472-481.
* indicates original appearance(s) of problem.
Drupal
CSI of Charles University