Home » Subject » Geometry
Importance: Medium ✭✭
Author(s): Kara, Jan
Por, Attila
Wood, David R.
Subject: Geometry
Keywords: Discrete Geometry
Geometric Ramsey Theory
Recomm. for undergrads: yes
Posted by: David Wood
on: September 25th, 2007

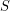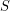Let $ S $ be a set of points in the plane. Two points $ v $ and $ w $ in $ S $ are visible with respect to 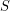$ S $ if the line segment between $ v $ and $ w $ contains no other point in $ S $.

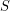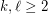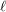Conjecture   For all integers $ k,\ell\geq2 $ there is an integer $ n $ such that every set of at least $ n $ points in the plane contains at least $ \ell $ collinear points or 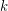$ k $ pairwise visible points.

The conjecture is trivial for 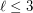$ \ell \leq 3 $.

Kára et al. [KPW] proved the conjecture for 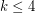$ k \leq 4 $ and all $ \ell $.

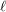Addario-Berry et al. [AFKCW] proved the conjecture for 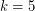$ k=5 $ and $ \ell=4 $.

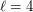Abel et al. [ABBCDHKLPW] proved the conjecture for 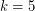$ k=5 $ and all $ \ell $.

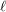The conjecture is open for 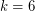$ k=6 $ or $ \ell=4 $.

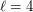Note that it is easily proved that for all 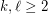$ k,\ell\geq2 $, every set of at least 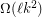$ \Omega(\ell k^2) $ points in the plane contains 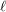$ \ell $ collinear points or 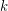$ k $ points with no three collinear [Brass].

See [Matousek] for related results and questions.

Bibliography

[ABBCDHKLPW] Zachary Abel, Brad Ballinger, Prosenjit Bose, Sébastien Collette, Vida Dujmović, Ferran Hurtado, Scott D. Kominers, Stefan Langerman, Attila Pór, David R. Wood. Every Large Point Set contains Many Collinear Points or an Empty Pentagon, Graphs and Combinatorics 27(1): 47-60, 2011.

[AFKCW] Louigi Addario-Berry, Cristina Fernandes, Yoshiharu Kohayakawa, Jos Coelho de Pina, and Yoshiko Wakabayashi. On a geometric Ramsey-style problem, 2007.

[Brass] Peter Brass. On point sets without k collinear points. In Discrete Geometry, vol. 253 of Monographs and Textbooks in Pure and Applied Mathematics, pp. 185–192. Dekker, New York, 2003.

*[KPW] Jan Kára, Attila Pór, David R. Wood. On the chromatic number of the visibility graph of a set of points in the plane, Discrete and Computational Geometry 34(3):497-506, 2005.

[Matousek] Jiří Matoušek. Blocking visibility for points in general position, Discrete and Computational Geometry 42(2): 219-223, 2009.


* indicates original appearance(s) of problem.
1 comment

Reply

Comments are limited to a maximum of 1000 characters.
More information about formatting options