 login/create account
login/create account
The stubborn list partition problem ★★
Author(s): Cameron; Eschen; Hoang; Sritharan
Problem Does there exist a polynomial time algorithm which takes as input a graph  and for every vertex
and for every vertex 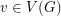 a subset
a subset 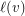 of
of 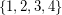 , and decides if there exists a partition of
, and decides if there exists a partition of 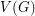 into
into 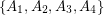 so that
so that 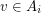 only if
only if 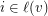 and so that
and so that 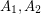 are independent,
are independent, 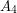 is a clique, and there are no edges between
is a clique, and there are no edges between 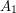 and
and 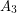 ?
?
 and for every vertex
and for every vertex 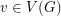 a subset
a subset 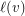 of
of 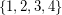 , and decides if there exists a partition of
, and decides if there exists a partition of 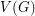 into
into 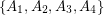 so that
so that 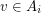 only if
only if 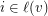 and so that
and so that 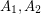 are independent,
are independent, 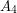 is a clique, and there are no edges between
is a clique, and there are no edges between 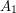 and
and 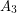 ?
? Keywords: list partition; polynomial algorithm
What is the largest graph of positive curvature? ★
Problem What is the largest connected planar graph of minimum degree 3 which has everywhere positive combinatorial curvature, but is not a prism or antiprism?
Keywords: curvature; planar graph
Few subsequence sums in Z_n x Z_n ★★
Conjecture For every 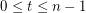 , the sequence in
, the sequence in 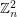 consisting of
consisting of 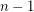 copes of
copes of 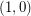 and
and 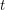 copies of
copies of 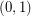 has the fewest number of distinct subsequence sums over all zero-free sequences from
has the fewest number of distinct subsequence sums over all zero-free sequences from 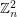 of length
of length 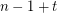 .
.
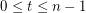 , the sequence in
, the sequence in 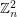 consisting of
consisting of 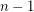 copes of
copes of 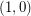 and
and 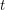 copies of
copies of 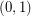 has the fewest number of distinct subsequence sums over all zero-free sequences from
has the fewest number of distinct subsequence sums over all zero-free sequences from 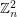 of length
of length 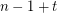 .
. Keywords: subsequence sum; zero sum
Olson's Conjecture ★★
Author(s): Olson
Conjecture If 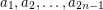 is a sequence of elements from a multiplicative group of order
is a sequence of elements from a multiplicative group of order  , then there exist
, then there exist 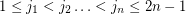 so that
so that 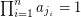 .
.
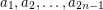 is a sequence of elements from a multiplicative group of order
is a sequence of elements from a multiplicative group of order  , then there exist
, then there exist 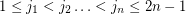 so that
so that 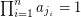 .
. Keywords: zero sum
Highly connected graphs with no K_n minor ★★★
Author(s): Thomas
Problem Is it true for all 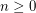 , that every sufficiently large
, that every sufficiently large  -connected graph without a
-connected graph without a 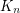 minor has a set of
minor has a set of 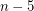 vertices whose deletion results in a planar graph?
vertices whose deletion results in a planar graph?
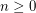 , that every sufficiently large
, that every sufficiently large  -connected graph without a
-connected graph without a 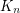 minor has a set of
minor has a set of 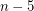 vertices whose deletion results in a planar graph?
vertices whose deletion results in a planar graph? Keywords: connectivity; minor
The Alon-Tarsi basis conjecture ★★
Author(s): Alon; Linial; Meshulam
Conjecture If 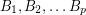 are invertible
are invertible 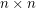 matrices with entries in
matrices with entries in 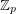 for a prime
for a prime 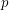 , then there is a
, then there is a 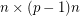 submatrix
submatrix  of
of ![$ [B_1 B_2 \ldots B_p] $](/files/tex/86661dc2948aeca789b4392c2e2a9cbf7d96f735.png) so that
so that  is an AT-base.
is an AT-base.
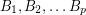 are invertible
are invertible 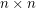 matrices with entries in
matrices with entries in 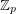 for a prime
for a prime 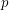 , then there is a
, then there is a 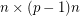 submatrix
submatrix  of
of ![$ [B_1 B_2 \ldots B_p] $](/files/tex/86661dc2948aeca789b4392c2e2a9cbf7d96f735.png) so that
so that  is an AT-base.
is an AT-base. Keywords: additive basis; matrix
The permanent conjecture ★★
Author(s): Kahn
Conjecture If  is an invertible
is an invertible 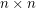 matrix, then there is an
matrix, then there is an 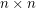 submatrix
submatrix 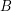 of
of ![$ [A A] $](/files/tex/d1e9d82c656535b507686183e640178057fae455.png) so that
so that 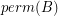 is nonzero.
is nonzero.
 is an invertible
is an invertible 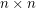 matrix, then there is an
matrix, then there is an 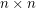 submatrix
submatrix 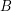 of
of ![$ [A A] $](/files/tex/d1e9d82c656535b507686183e640178057fae455.png) so that
so that 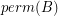 is nonzero.
is nonzero. Keywords: invertible; matrix; permanent
The additive basis conjecture ★★★
Author(s): Jaeger; Linial; Payan; Tarsi
Conjecture For every prime 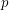 , there is a constant
, there is a constant 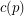 (possibly
(possibly 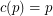 ) so that the union (as multisets) of any
) so that the union (as multisets) of any 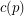 bases of the vector space
bases of the vector space 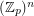 contains an additive basis.
contains an additive basis.
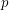 , there is a constant
, there is a constant 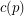 (possibly
(possibly 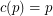 ) so that the union (as multisets) of any
) so that the union (as multisets) of any 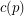 bases of the vector space
bases of the vector space 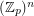 contains an additive basis.
contains an additive basis. Keywords: additive basis; matrix

 Drupal
Drupal CSI of Charles University
CSI of Charles University