Open Problem Garden

Roller Coaster permutations ★★★

Let $S_n$ denote the set of all permutations of $[n]=\set{1,2,\ldots,n}$ . Let $i(\pi)$ and $d(\pi)$ denote respectively the number of increasing and the number of decreasing sequences of contiguous numbers in $\pi$ . Let $X(\pi)$ denote the set of subsequences of $\pi$ with length at least three. Let $t(\pi)$ denote $\sum_{\tau\in X(\pi)}(i(\tau)+d(\tau))$ .

A permutation $\pi\in S_n$ is called a Roller Coaster permutation if $t(\pi)=\max_{\tau\in S_n}t(\tau)$ . Let $RC(n)$ be the set of all Roller Coaster permutations in $S_n$ .

Conjecture For $n\geq 3$ ,

$n=2k$

$|RC(n)|=4$

$n=2k+1$

$|RC(n)|=2^j$

$j\leq k+1$

Conjecture (Odd Sum conjecture) Given $\pi\in RC(n)$ ,

$n=2k+1$

$\pi_j+\pi_{n-j+1}$

$1\leq j\leq k$

$n=2k$

$\pi_j + \pi_{n-j+1} = 2k+1$

$1\leq j\leq k$

Keywords:

Posted by Tanbir Ahmed
updated October 14th, 2013

add new comment

cycle spectrum

Alban Henri

remove nsf security, nsf security remover, steps to open notes files

Adel P. Kazemi

Total dominator chromatic number, hypercube.

Graph Theory » Coloring » Vertex coloring

Total Dominator Chromatic Number of a Hypercube ★★

Author(s): Adel P. Kazemi

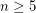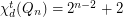Conjecture For any integer $n\geq 5$ , $\chi_d^t(Q_n)=2^{n-2}+2$ .

Keywords: Total dominator chromatic number, hypercube.

Posted by Adel P. Kazemi
updated November 1st, 2014

1 comment

Total domination number, Hypercube

Graph Theory » Basic G.T.

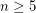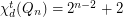Total Domination number of a hypercube ★★★

Author(s): Adel P. Kazemi

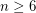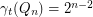Conjecture For any integer $n\geq 6$ , $\gamma_t(Q_n) = 2^{n-2}$ .

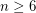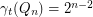Keywords: Total domination number, Hypercube

Posted by Adel P. Kazemi
updated November 30th, 2013

1 comment

Algebra

Graphs of exact colorings ★★

Author(s):

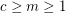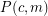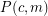Conjecture For $c \geq m \geq 1$ , let $P(c,m)$ be the statement that given any exact $c$ -coloring of the edges of a complete countably infinite graph (that is, a coloring with $c$ colors all of which must be used at least once), there exists an exactly $m$ -colored countably infinite complete subgraph. Then $P(c,m)$ is true if and only if 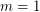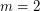$m=1$ , $m=2$ , or $c=m$ .