 login/create account
login/create account
Covering powers of cycles with equivalence subgraphs
 and
and  , the graph
, the graph  has equivalence covering number
has equivalence covering number 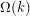 .
.
Given a graph  , a subgraph
, a subgraph  of
of  is an equivalence subgraph of
is an equivalence subgraph of  if
if  a disjoint union of cliques. The quivalence covering number of
a disjoint union of cliques. The quivalence covering number of  , denoted
, denoted  , is the least number of equivalence subgraphs needed to cover the edges of
, is the least number of equivalence subgraphs needed to cover the edges of  .
.
This problem has been studied by various people since the 80s [A]. For line graphs, the equivalence covering number is known to within a constant factor [EGK]. It is therefore tempting to examine the situation for quasi-line graphs and claw-free graphs. Powers of cycles are perhaps the simplest interesting class of claw-free graphs that are not necessarily line graphs. However, even for  very large compared to
very large compared to  , no upper bound is known beyond trivial linear bounds of order
, no upper bound is known beyond trivial linear bounds of order 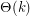 . Furthermore, it is not even certain that a nontrivial lower bound (i.e. going to infinity as
. Furthermore, it is not even certain that a nontrivial lower bound (i.e. going to infinity as  goes to infinity) is known. It is possible that this can be related somehow to a known result, but for now it seems at least superficially that this problem is wide open.
goes to infinity) is known. It is possible that this can be related somehow to a known result, but for now it seems at least superficially that this problem is wide open.
Bibliography
[A] N. Alon, Covering graphs with the minimum number of equivalence relations, Combinatorica 6 (1986) 201–206.
[EGK] L. Esperet, J. Gimbel, A. King, Covering line graphs with equivalence relations, Discrete Applied Mathematics Volume 158, Issue 17, 28 October 2010, Pages 1902-1907.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University