 login/create account
login/create account
Multicolour Erdős--Hajnal Conjecture
Conjecture For every fixed 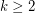 and fixed colouring
and fixed colouring 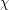 of
of 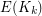 with
with  colours, there exists
colours, there exists 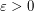 such that every colouring of the edges of
such that every colouring of the edges of 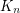 contains either
contains either  vertices whose edges are coloured according to
vertices whose edges are coloured according to 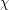 or
or 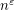 vertices whose edges are coloured with at most
vertices whose edges are coloured with at most 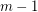 colours.
colours.
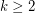 and fixed colouring
and fixed colouring 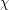 of
of 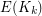 with
with  colours, there exists
colours, there exists 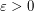 such that every colouring of the edges of
such that every colouring of the edges of 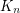 contains either
contains either  vertices whose edges are coloured according to
vertices whose edges are coloured according to 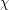 or
or 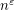 vertices whose edges are coloured with at most
vertices whose edges are coloured with at most 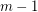 colours.
colours. See [FGP].
Bibliography
[FGP] Jacob Fox, Andrey Grinshpun and János Pach: The Erdős–Hajnal conjecture for rainbow triangles, J. Combin. Theory, Series B. 111 (2016), 75--125.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University