 login/create account
login/create account
Erickson, Martin
Transversal achievement game on a square grid ★★
Author(s): Erickson
Problem Two players alternately write O's (first player) and X's (second player) in the unoccupied cells of an 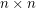 grid. The first player (if any) to occupy a set of
grid. The first player (if any) to occupy a set of  cells having no two cells in the same row or column is the winner. What is the outcome of the game given optimal play?
cells having no two cells in the same row or column is the winner. What is the outcome of the game given optimal play?
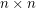 grid. The first player (if any) to occupy a set of
grid. The first player (if any) to occupy a set of  cells having no two cells in the same row or column is the winner. What is the outcome of the game given optimal play?
cells having no two cells in the same row or column is the winner. What is the outcome of the game given optimal play? Keywords: game
Exact colorings of graphs ★★
Author(s): Erickson
Conjecture For 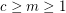 , let
, let 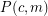 be the statement that given any exact
be the statement that given any exact  -coloring of the edges of a complete countably infinite graph (that is, a coloring with
-coloring of the edges of a complete countably infinite graph (that is, a coloring with  colors all of which must be used at least once), there exists an exactly
colors all of which must be used at least once), there exists an exactly  -colored countably infinite complete subgraph. Then
-colored countably infinite complete subgraph. Then 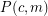 is true if and only if
is true if and only if 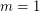 ,
, 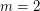 , or
, or  .
.
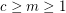 , let
, let 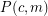 be the statement that given any exact
be the statement that given any exact  -coloring of the edges of a complete countably infinite graph (that is, a coloring with
-coloring of the edges of a complete countably infinite graph (that is, a coloring with  colors all of which must be used at least once), there exists an exactly
colors all of which must be used at least once), there exists an exactly  -colored countably infinite complete subgraph. Then
-colored countably infinite complete subgraph. Then 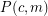 is true if and only if
is true if and only if 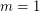 ,
, 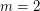 , or
, or  .
. Keywords: graph coloring; ramsey theory
Square achievement game on an n x n grid ★★
Author(s): Erickson
Problem Two players alternately write O's (first player) and X's (second player) in the unoccupied cells of an 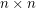 grid. The first player (if any) to occupy four cells at the vertices of a square with horizontal and vertical sides is the winner. What is the outcome of the game given optimal play? Note: Roland Bacher and Shalom Eliahou proved that every 15 x 15 binary matrix contains four equal entries (all 0's or all 1's) at the vertices of a square with horizontal and vertical sides. So the game must result in a winner (the first player) when n=15.
grid. The first player (if any) to occupy four cells at the vertices of a square with horizontal and vertical sides is the winner. What is the outcome of the game given optimal play? Note: Roland Bacher and Shalom Eliahou proved that every 15 x 15 binary matrix contains four equal entries (all 0's or all 1's) at the vertices of a square with horizontal and vertical sides. So the game must result in a winner (the first player) when n=15.
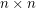 grid. The first player (if any) to occupy four cells at the vertices of a square with horizontal and vertical sides is the winner. What is the outcome of the game given optimal play? Note: Roland Bacher and Shalom Eliahou proved that every 15 x 15 binary matrix contains four equal entries (all 0's or all 1's) at the vertices of a square with horizontal and vertical sides. So the game must result in a winner (the first player) when n=15.
grid. The first player (if any) to occupy four cells at the vertices of a square with horizontal and vertical sides is the winner. What is the outcome of the game given optimal play? Note: Roland Bacher and Shalom Eliahou proved that every 15 x 15 binary matrix contains four equal entries (all 0's or all 1's) at the vertices of a square with horizontal and vertical sides. So the game must result in a winner (the first player) when n=15. Keywords: game
Sequence defined on multisets ★★
Author(s): Erickson
Conjecture Define a 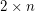 array of positive integers where the first row consists of some distinct positive integers arranged in increasing order, and the second row consists of any positive integers in any order. Create a new array where the first row consists of all the integers that occur in the first array, arranged in increasing order, and the second row consists of their multiplicities. Repeat the process. For example, starting with the array
array of positive integers where the first row consists of some distinct positive integers arranged in increasing order, and the second row consists of any positive integers in any order. Create a new array where the first row consists of all the integers that occur in the first array, arranged in increasing order, and the second row consists of their multiplicities. Repeat the process. For example, starting with the array ![$ [1; 1] $](/files/tex/73f8649de444361674c157a2fe98e0c5783f1c46.png) , the sequence is:
, the sequence is: ![$ [1; 1] $](/files/tex/73f8649de444361674c157a2fe98e0c5783f1c46.png) ->
-> ![$ [1; 2] $](/files/tex/83c3d9d7589f716ed6b0f05d26d36dabe8ba47aa.png) ->
-> ![$ [1, 2; 1, 1] $](/files/tex/a6a696aec4e84df6bc046cf6d30a4df80e156a14.png) ->
-> ![$ [1, 2; 3, 1] $](/files/tex/98b2f3e4134422c8a286f0326fc2f57ca9be2ab7.png) ->
-> ![$ [1, 2, 3; 2, 1, 1] $](/files/tex/19a9d24510f4551fa45b950aed32efed0636b355.png) ->
-> ![$ [1, 2, 3; 3, 2, 1] $](/files/tex/b00d573110ba8c2472820409103dd4cbd7bff7cc.png) ->
-> ![$ [1, 2, 3; 2, 2, 2] $](/files/tex/2aae90b65ae3f116402a1c0143127f80d86acdf0.png) ->
-> ![$ [1, 2, 3; 1, 4, 1] $](/files/tex/d614399c4078a70fbffb24eb99816a0974423175.png) ->
-> ![$ [1, 2, 3, 4; 3, 1, 1, 1] $](/files/tex/bf4dd82eaf95bd71a88cb78d3367efa2c7e4c942.png) ->
-> ![$ [1, 2, 3, 4; 4, 1, 2, 1] $](/files/tex/a4ef5900a9dde9b32311afe7dee2b143f42c405f.png) ->
-> ![$ [1, 2, 3, 4; 3, 2, 1, 2] $](/files/tex/ff367376ed7bb74fc6207273d7157062b83a1be6.png) ->
-> ![$ [1, 2, 3, 4; 2, 3, 2, 1] $](/files/tex/81ba2b3608ddba2fc95d32b74b70279f3f5adc5b.png) , and we now have a fixed point (loop of one array).
, and we now have a fixed point (loop of one array).
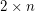 array of positive integers where the first row consists of some distinct positive integers arranged in increasing order, and the second row consists of any positive integers in any order. Create a new array where the first row consists of all the integers that occur in the first array, arranged in increasing order, and the second row consists of their multiplicities. Repeat the process. For example, starting with the array
array of positive integers where the first row consists of some distinct positive integers arranged in increasing order, and the second row consists of any positive integers in any order. Create a new array where the first row consists of all the integers that occur in the first array, arranged in increasing order, and the second row consists of their multiplicities. Repeat the process. For example, starting with the array ![$ [1; 1] $](/files/tex/73f8649de444361674c157a2fe98e0c5783f1c46.png) , the sequence is:
, the sequence is: ![$ [1; 1] $](/files/tex/73f8649de444361674c157a2fe98e0c5783f1c46.png) ->
-> ![$ [1; 2] $](/files/tex/83c3d9d7589f716ed6b0f05d26d36dabe8ba47aa.png) ->
-> ![$ [1, 2; 1, 1] $](/files/tex/a6a696aec4e84df6bc046cf6d30a4df80e156a14.png) ->
-> ![$ [1, 2; 3, 1] $](/files/tex/98b2f3e4134422c8a286f0326fc2f57ca9be2ab7.png) ->
-> ![$ [1, 2, 3; 2, 1, 1] $](/files/tex/19a9d24510f4551fa45b950aed32efed0636b355.png) ->
-> ![$ [1, 2, 3; 3, 2, 1] $](/files/tex/b00d573110ba8c2472820409103dd4cbd7bff7cc.png) ->
-> ![$ [1, 2, 3; 2, 2, 2] $](/files/tex/2aae90b65ae3f116402a1c0143127f80d86acdf0.png) ->
-> ![$ [1, 2, 3; 1, 4, 1] $](/files/tex/d614399c4078a70fbffb24eb99816a0974423175.png) ->
-> ![$ [1, 2, 3, 4; 3, 1, 1, 1] $](/files/tex/bf4dd82eaf95bd71a88cb78d3367efa2c7e4c942.png) ->
-> ![$ [1, 2, 3, 4; 4, 1, 2, 1] $](/files/tex/a4ef5900a9dde9b32311afe7dee2b143f42c405f.png) ->
-> ![$ [1, 2, 3, 4; 3, 2, 1, 2] $](/files/tex/ff367376ed7bb74fc6207273d7157062b83a1be6.png) ->
-> ![$ [1, 2, 3, 4; 2, 3, 2, 1] $](/files/tex/81ba2b3608ddba2fc95d32b74b70279f3f5adc5b.png) , and we now have a fixed point (loop of one array).
, and we now have a fixed point (loop of one array).
The process always results in a loop of 1, 2, or 3 arrays.

 Drupal
Drupal CSI of Charles University
CSI of Charles University