 login/create account
login/create account
Hall, Marshall
Hall-Paige conjecture ★★★
A complete map for a (multiplicative) group  is a bijection
is a bijection 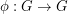 so that the map
so that the map 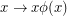 is also a bijection.
is also a bijection.
Conjecture If  is a finite group and the Sylow 2-subgroups of
is a finite group and the Sylow 2-subgroups of  are either trivial or non-cyclic, then
are either trivial or non-cyclic, then  has a complete map.
has a complete map.
 is a finite group and the Sylow 2-subgroups of
is a finite group and the Sylow 2-subgroups of  are either trivial or non-cyclic, then
are either trivial or non-cyclic, then  has a complete map.
has a complete map. Keywords: complete map; finite group; latin square

 Drupal
Drupal CSI of Charles University
CSI of Charles University