Home » Author index

Pach, János


Graph Theory » Extremal G.T.

Odd-cycle transversal in triangle-free graphs ★★

Author(s): Erdos; Faudree; Pach; Spencer

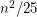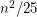Conjecture   If $ G $ is a simple triangle-free graph, then there is a set of at most $ n^2/25 $ edges whose deletion destroys every odd cycle.

Keywords:

Posted by fhavet
updated March 6th, 2013
add new comment
Graph Theory » Topological G.T. » Crossing numbers

Are different notions of the crossing number the same? ★★★

Author(s): Pach; Tóth

Problem   Does the following equality hold for every graph $ G $? \[ \text{pair-cr}(G) = \text{cr}(G) \]

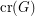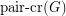The crossing number $ \text{cr}(G) $ of a graph $ G $ is the minimum number of edge crossings in any drawing of $ G $ in the plane. In the pairwise crossing number $ \text{pair-cr}(G) $, we minimize the number of pairs of edges that cross.

Keywords: crossing number; pair-crossing number

Posted by cibulka
updated November 3rd, 2009
add new comment
Syndicate content