Home » Subject » Graph Theory » Basic G.T. » Cycles
Importance: High ✭✭✭
Author(s): Celmins, Uldis A.
Preissmann, Myriam
Subject: Graph Theory
» Basic Graph Theory
» » Cycles
Keywords: cover
cycle
Recomm. for undergrads: no
Posted by: mdevos
on: March 7th, 2007
Conjecture   Every bridgeless graph has a (5,2)-cycle-cover.

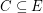Definition: If $ G=(V,E) $ is a graph, a binary cycle of $ G $ is a set $ C \subseteq E $ such that every vertex of the graph 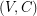$ (V,C) $ has even degree. An 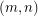$ (m,n) $-cycle-cover of $ G $ is a list $ L $ consisting of $ m $ cycles so that every edge of $ G $ is contained in exactly $ n $ of these cycles.

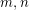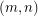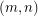Since every binary cycle can be written as a disjoint union of edge sets of ordinary cycles, the above conjecture is a strengthening of the cycle double cover conjecture. For positive integers $ m,n $ it is natural to ask what family of graphs have $ (m,n) $-cycle-covers. The following chart gives some information about this question for small values of $ m $ and $ n $. A "yes" in the $ (m,n) $ box indicates that every graph with no cut-edge has an 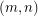$ (m,n) $-cycle-cover. A "no" indicates that no graph has an 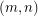$ (m,n) $-cycle-cover. A more detailed explanation of the entries in this chart appears below it.

m
n

2 3 4 5 6 7 8 9 10 11
2 Eulerian NZ 4-flow NZ 4-flow 5CDC conj open
4 no Eulerian 5 post. sets B-F conj yes [BJJ] yes
6 no Eulerian 7 post. sets ? ? yes [F] yes

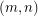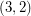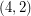We did not include odd values of n, since any graph with an $ (m,n) $-cycle-cover for an odd integer $ n $ must be Eulerian. The entry "NZ 4-flow" is short for nowhere-zero 4-flow. Thus, our chart indicates that ($ G $ has a nowhere-zero 4-flow) if and only if ($ G $ has a $ (3,2) $-cycle-cover) if and only if ($ G $ has a $ (4,2) $-cycle-cover). These equivalences were discovered by Tutte [Tu].

Two of the 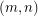$ (m,n) $ boxes are conjectures. The 5CDC conj is the 5 cycle double cover conjecture and the B-F conjecture is the Berge-Fulkerson conjecture. In both of these cases, the conjecture is equivalent to the assertion that every graph with no cut-edge has an 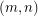$ (m,n) $-cycle-cover (i.e. it would be accurate to put a "yes" in the corresponding. box). For emphasis, we state the Berge-Fulkerson conjecture again below in this new form.

Conjecture  (The Berge-Fulkerson conjecture)   Every graph with no cut-edge has a (6,4)-cycle-cover.

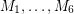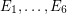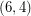The fact that the above conjecture is equivalent to the usual statement of the Berge-Fulkerson conjecture was discovered by Jaeger [J]. For cubic graphs this equivalence is easy to see, since $ M_1,\ldots,M_6 $ satisfy the Berge-Fulkerson conjecture if and only if $ E\M_1,\ldots,E\M_6 $ is a $ (6,4) $-cycle-cover. 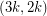By Jaeger's argument, the weak Berge-Fulkerson conjecture is equivalent to the statement that there exists a fixed integer $ k $ so that every bridgeless graph has a $ (3k,2k) $-cycle-cover.

A postman set is a set of edges 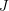$ J $ such that 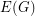$ E(G)\J $ is a cycle. The entry "k post. sets" in the 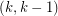$ (k,k-1) $ box of the above chart indicates that a graph G has a 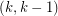$ (k,k-1) $-cycle-cover if and only if it is possible to partition the edges of $ G $ into $ k $ postman sets. This equivalence follows immediately from the definition. Rizzi's Packing postman sets conjecture is thus equivalent to the following conjecture on cycle-covers.

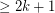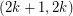Conjecture  (the packing postman sets conjecture)   If every odd edge-cut of $ G $ has size $ \ge 2k+1 $, then $ G $ has a $ (2k+1,2k) $-cycle-cover.

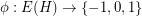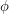Next we turn our attention to orientable cycle covers. If $ H $ is a directed graph a map $ \phi:E(H) \rightarrow \{-1,0,1\} $ is a 2-flow or an oriented cycle if at every vertex of $ H $, the sum of $ \phi $ on the incoming edges is equal to the sum of 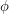$ \phi $ on the outgoing edges. It is easy to see that the support of a 2-flow is always a cycle. 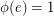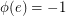Furthermore, for any oriented cycle, there is a list $ L $ of edge-disjoint circuits with directions so that an edge $ e $ is forward (backward) in a circuit of $ L $ if and only if $ \phi(e)=1 $ ($ \phi(e)=-1 $). So as in the unoriented case, an oriented cycle may be viewed as the edge-disjoint union of oriented circuits. 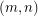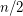For an even integer $ n $, a $ (m,n) $-oriented-cycle-cover of a graph $ G $ is a list of $ m $ oriented cycles so that every edge of $ G $ appears as a forward edge $ n/2 $ times and a backward edge 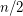$ n/2 $ times. The following conjecture is the common generalization of the orientable cycle double cover conjecture and the five cycle double cover conjecture. It is due to Archdeacon and Jaeger.

Conjecture  (The orientable five cycle double cover conjecture)   Every graph without a cut-edge has a (5,2)-oriented-cycle-cover.

Considerably less is known about 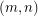$ (m,n) $-oriented-cycle-covers. We sumarize some of what is known for small values of $ m $ and $ n $ below.

m
n

2 3 4 5 6 7 8 9 10 11
2 Eulerian NZ 3-flow NZ 4-flow O5CDC conj open
4 no Eulerian ? ? ? conj. open
6 no Eulerian ? ? ? ? yes [DG]

Every graph with an 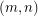$ (m,n) $-cycle-cover also has a 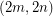$ (2m,2n) $-oriented-cycle-cover obtained by taking two copies of each cycle with opposite orientations. Thus, by Bermond, Jackson, and Jaeger's 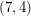$ (7,4) $-cycle-cover theorem, every bridgeless graph with no has a 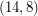$ (14,8) $-oriented-cycle-cover. DeVos and Goddyn have observed that Seymour's 6-flow theorem can be used to construct an 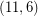$ (11,6) $-oriented-cycle-cover for every bridgeless graph. 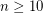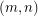By combining these, we find that for every even integer $ n \ge 10 $ there exists an $ m $ so that every bridgeless graph has an $ (m,n) $-oriented-cycle-cover. 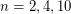This question is still open for $ n=2,4,10 $.

The following conjecture appears in the above chart.

Conjecture  (The orientable eight cycle four cover conjecture)   Every graph with no cut-edge has a (8,4)-oriented-cycle-cover.

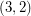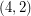This conjecture may be viewed as a sort of oriented version of the Berge-Fulkerson conjecture. To see this analogy, note that ($ G $ has a nowhere-zero 4-flow) if and only if ($ G $ has a $ (3,2) $-cycle-cover) if and only if ($ G $ has a $ (4,2) $-oriented-cycle-cover). The Berge-Fulkerson conjecture and the above conjecture assert respectively that every bridgeless graph has a 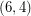$ (6,4) $-cycle-cover and a 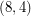$ (8,4) $-oriented-cycle-cover (i.e. a cover with double the parameters which are equivalent to a nowhere-zero 4-flow). As with most of the conjectures in this area, the above conjecture is trivially true for graphs with nowhere-zero 4-flows and it holds for the Petersen graph.

Bibliography

[A] D. Archdeacon, Face coloring of embedded graphs. J. Graph Theory, 8(1984), 387-398.

[BJJ] J.C. Bermond, B. Jackson, and F. Jaeger, Shortest covering of graphs with cycles, J. Combinatorial Theory Ser. B 35 (1983), 297-308. MathSciNet

*[C] A. U. Celmins, On cubic graphs that do not have an edge-3-colouring, Ph.D. Thesis, Department of Combinatorics and Optimization, University of Waterloo, Waterloo, Canada, 1984.

[F] G. Fan, Integer flows and cycle covers, J. Combinatorial Theory Ser. B 54 (1992), 113-122. MathSciNet

[J] F. Jaeger, Flows and Generalized Coloring Theorems in Graphs, J. Combinatorial Theory Ser. B 26 (1979) 205-216. MathSciNet

[J88] F. Jaeger, Nowhere zero flow problems. Selected Topics in Graph Theory 3 (L.W.Beineke and R.J.Wilson eds.), Academic Press, London (1988), 71-95.

*[P] M. Preissmann, Sur les colorations des arêtes des graphes cubiques, Thèse de 3ème cycle, Grenoble (1981) .

[T54] W.T. Tutte, A Contribution on the Theory of Chromatic Polynomials, Canad. J. Math. 6 (1954) 80-91. MathSciNet

[T66] W.T. Tutte, On the Algebraic Theory of Graph Colorings, J. Combinatorial Theory 1 (1966) 15-50. MathSciNet


* indicates original appearance(s) of problem.
add new comment

Reply

Comments are limited to a maximum of 1000 characters.
More information about formatting options