Home » Subject » Combinatorics » Ramsey Theory
Importance: High ✭✭✭
Author(s): Brown, Tom C.
Graham, Ronald L.
Landman, Bruce M.
Subject: Combinatorics
» Ramsey Theory
Keywords: 2-large sets
large sets
Recomm. for undergrads: no
Posted by: vjungic
on: June 10th, 2007
Conjecture   If $ A $ is 2-large, then $ A $ is large.

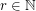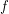For $ r\in \mathbb{N} $, a set of positive integers $ L $ is said to be $ r $-large if for any $ r $-coloring $ f $ of positive integers there are arbitrarily long 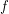$ f $ - monochromatic arithmetic progressions whose common differences belong to $ L $. Then $ L $ is large if and only if it is $ r $-large for all $ r $. 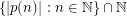From Bergelson-Leibman's Polynomial van der Waerden's Theorem [BL] it follows that $ \{ |p(n)| : n \in \mathbb{N} \} \cap \mathbb{N} $ is large for any polynomal 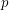$ p $ with rational coefficients and such that $ p(0)=0 $.

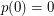The conjecture was stated in 1995 and published in 1999 [BGL].

Bibliography

[BL] V. Bergelson and A. Leibman, Polynomial extension of van der Waerden’s and Szemer\'{e}di’s theorems, J. Amer. Math. Soc. 9 (1996) 725-753.

*[BGL] T.C. Brown, R. L. Graham, and B. M. Landman, On the set of common differences in van der Waerden’s theorem on arithmetic progressions, Canadian Math. Bull. 42 (1999) 25-36.

[J] V. Jungic, On Brown’s conjecture on Accessible Sets, J. Comb. Theory, Ser. A 110(1) (2005), 175-178

[LR] B. M. Landman and A. Robertson, Ramsey Theory on the Integers, American Mathematical Society, 2004.


* indicates original appearance(s) of problem.
add new comment

Reply

Comments are limited to a maximum of 1000 characters.
More information about formatting options