 login/create account
login/create account
Conjecture The poset of multifuncoids of the form 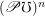 is for every sets
is for every sets 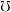 and
and  :
:
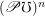 is for every sets
is for every sets 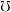 and
and  :
:- \item atomic; \item atomistic.
See below for definition of all concepts and symbols used to in this conjecture.
Refer to this Web site for the theory which I now attempt to generalize.
Definition A free star on a join-semilattice 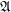 with least element 0 is a set
with least element 0 is a set 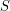 such that
such that  and
and ![\[ \forall A, B \in \mathfrak{A}: \left( A \cup B \in S \Leftrightarrow A \in S \vee B \in S \right) . \]](/files/tex/70420d16ddf609e4c505908182520a5bcf379d3e.png)
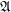 with least element 0 is a set
with least element 0 is a set 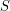 such that
such that  and
and ![\[ \forall A, B \in \mathfrak{A}: \left( A \cup B \in S \Leftrightarrow A \in S \vee B \in S \right) . \]](/files/tex/70420d16ddf609e4c505908182520a5bcf379d3e.png)
Definition Let 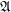 be a family of posets,
be a family of posets, 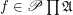 (
(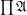 has the order of function space of posets),
has the order of function space of posets), 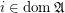 ,
, 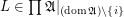 . Then
. Then ![\[ \left( \ensuremath{\operatorname{val}}f \right)_i L = \left\{ X \in \mathfrak{A}_i \hspace{0.5em} | \hspace{0.5em} L \cup \left\{ (i ; X) \right\} \in f \right\} . \]](/files/tex/402ce92b70bfd908eefa69f8ec7f3b5cd3cb72d2.png)
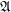 be a family of posets,
be a family of posets, 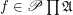 (
(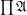 has the order of function space of posets),
has the order of function space of posets), 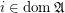 ,
, 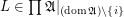 . Then
. Then ![\[ \left( \ensuremath{\operatorname{val}}f \right)_i L = \left\{ X \in \mathfrak{A}_i \hspace{0.5em} | \hspace{0.5em} L \cup \left\{ (i ; X) \right\} \in f \right\} . \]](/files/tex/402ce92b70bfd908eefa69f8ec7f3b5cd3cb72d2.png)
Definition Let 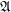 is a family of posets. A multidimensional funcoid (or multifuncoid for short) of the form
is a family of posets. A multidimensional funcoid (or multifuncoid for short) of the form 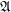 is an
is an 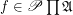 such that we have that:
such that we have that:
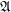 is a family of posets. A multidimensional funcoid (or multifuncoid for short) of the form
is a family of posets. A multidimensional funcoid (or multifuncoid for short) of the form 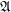 is an
is an 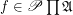 such that we have that:
such that we have that:- \item
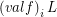 is a free star for every
is a free star for every 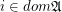 ,
, 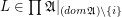 .
.
\item 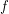 is an upper set.
is an upper set.
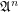 is a function space over a poset
is a function space over a poset 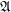 that is
that is 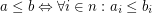 for
for  .
.
Bibliography
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University