 login/create account
login/create account
An directed graph is  -diregular if every vertex has indegree and outdegree at least
-diregular if every vertex has indegree and outdegree at least  .
.
Conjecture For 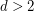 , every
, every 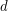 -diregular oriented graph on at most
-diregular oriented graph on at most 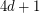 vertices has a Hamilton cycle.
vertices has a Hamilton cycle.
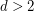 , every
, every 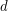 -diregular oriented graph on at most
-diregular oriented graph on at most 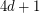 vertices has a Hamilton cycle.
vertices has a Hamilton cycle. The disjoint union of two regular tournaments on 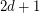 vertices shows that this would be best possible. For
vertices shows that this would be best possible. For 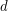 -diregular oriented graphs with an arbitrary order of vertices, Jackson conjectured the existence of a long cycle.
-diregular oriented graphs with an arbitrary order of vertices, Jackson conjectured the existence of a long cycle.
Kühn and Osthus [KO] conjectured that it may actually be possible to increase the size of the graph even further if we assume that the graph is strongly 2-connected.
Problem Is it true that for each 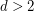 , every
, every 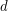 -regular strongly
-regular strongly 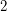 -connected oriented graph
-connected oriented graph  on at most
on at most 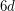 vertices has a Hamilton cycle?
vertices has a Hamilton cycle?
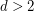 , every
, every 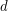 -regular strongly
-regular strongly 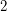 -connected oriented graph
-connected oriented graph  on at most
on at most 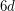 vertices has a Hamilton cycle?
vertices has a Hamilton cycle? Bibliography
*[J] B. Jackson. Long paths and cycles in oriented graphs, J. Graph Theory 5 (1981), 145-157.
[KO] D. Osthus and D. Kühn, A survey on Hamilton cycles in directed graphs, European J. Combinatorics 33 (2012), 750-766.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University