 login/create account
login/create account
Problem Find six positive integers 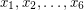 such that
such that 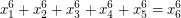 or prove that such integers do not exist.
or prove that such integers do not exist.
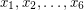 such that
such that 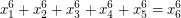 or prove that such integers do not exist.
or prove that such integers do not exist.
Euler's sum of powers conjecture states that for 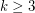 the Diophantine equation
the Diophantine equation 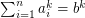 does not have solutions in positive integers as soon as
does not have solutions in positive integers as soon as  For
For 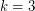 it corresponds to a particular case of Fermat Last Theorem and hence is true. For
it corresponds to a particular case of Fermat Last Theorem and hence is true. For 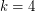 and
and 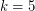 , counterexamples to the Euler's sum of powers conjecture were found by N. Elkies in 1986 and L. J. Lander, T. R. Parkin in 1966 respectively. For
, counterexamples to the Euler's sum of powers conjecture were found by N. Elkies in 1986 and L. J. Lander, T. R. Parkin in 1966 respectively. For 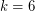 , no counterexamples are currently known.
, no counterexamples are currently known.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University