 login/create account
login/create account
 ,
,(a)
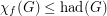
(b)
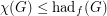
(c)
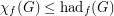 .
. Here 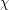 is the chromatic number,
is the chromatic number, 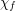 is the fractional chromatic number,
is the fractional chromatic number, 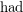 is the Hadwiger number, and
is the Hadwiger number, and 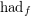 is the fractional Hadwiger number (which was recently introduced independently by Fox [F] and Pedersen [P]).
is the fractional Hadwiger number (which was recently introduced independently by Fox [F] and Pedersen [P]).
It is well known and easily proved (see [HW]) that
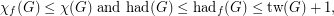
where 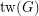 is the treewidth of
is the treewidth of  .
.
Hadwiger's famous conjecture, 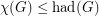 , bridges the gap in the above inequalities. The above conjectures therefore are weaker than Hadwiger's conjecture. Note that Conjecture (a) implies Conjecture (c), and Conjecture (b) implies Conjecture (c).
, bridges the gap in the above inequalities. The above conjectures therefore are weaker than Hadwiger's conjecture. Note that Conjecture (a) implies Conjecture (c), and Conjecture (b) implies Conjecture (c).
Note that Reed and Seymour [RS] proved that 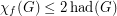 .
.
Conjecture (a) is due to Reed and Seymour [RS]. Conjecture (b) is due to Harvey and Wood [HW]. Conjecture (c) is independently due to Harvey and Wood [HW] and Pedersen [P].
Pedersen [P] presents a natural equivalent formulation of Conjecture (c).
Bibliography
*[HW] Daniel J. Harvey, David R. Wood, Parameters tied to treewidth. arXiv:1312.3401, 2013.
[F] Jacob Fox. Constructing dense graphs with sublinear Hadwiger number. J. Combin. Theory Ser. B (to appear).
*[P] Anders Sune Pedersen. Contributions to the Theory of Colourings, Graph Minors, and Independent Sets, PhD thesis, Department of Mathematics and Computer Science University of Southern Denmark, 2011.
*[RS] Bruce A. Reed, Paul D. Seymour, Fractional colouring and Hadwiger's conjecture. J. Combin. Theory Ser. B, 74(2), 147-152.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University