Actually, the conjecture is disproved by , obtained independently by Hougardy in 1991 [1] and Royle in 1993 [2, Section 9.7]. Moreover, although not fully determined, it is known that asymptotically attains the lower bound, as , proven by Ostergard in 2004 [3].
There are also several results on for general , and in particular on [3,4].
[1] G.M. Ziegler, Coloring Hamming graphs, optimal binary codes, and the 0/1 Borsuk problem in low dimensions, in: H. Alt (Ed.), Computational Discrete Mathematics, Springer, Berlin, 2001, 159-171.
[2] T.R. Jensen, B. Toft, Graph Coloring Problems, Wiley, New York, 1995.
[3] P.R.J. Ostergard, On a Hypercube coloring problem, J. Combin. Theory A 108 (2004), 199-204.
[4] H.Q. Ngo, D.-Z. Du, R.L. Graham, New bounds on a hypercube coloring problem, Inform. Process. Lett. 84 (2002), 265-269.
disproved
Actually, the conjecture is disproved by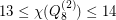 , obtained independently by Hougardy in 1991 [1] and Royle in 1993 [2, Section 9.7]. Moreover, although not fully determined, it is known that
, obtained independently by Hougardy in 1991 [1] and Royle in 1993 [2, Section 9.7]. Moreover, although not fully determined, it is known that 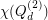 asymptotically attains the lower bound, as
asymptotically attains the lower bound, as 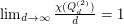 , proven by Ostergard in 2004 [3].
, proven by Ostergard in 2004 [3].
There are also several results on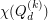 for general
for general 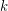 , and in particular on
, and in particular on 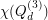 [3,4].
[3,4].
[1] G.M. Ziegler, Coloring Hamming graphs, optimal binary codes, and the 0/1 Borsuk problem in low dimensions, in: H. Alt (Ed.), Computational Discrete Mathematics, Springer, Berlin, 2001, 159-171.
[2] T.R. Jensen, B. Toft, Graph Coloring Problems, Wiley, New York, 1995.
[3] P.R.J. Ostergard, On a Hypercube coloring problem, J. Combin. Theory A 108 (2004), 199-204.
[4] H.Q. Ngo, D.-Z. Du, R.L. Graham, New bounds on a hypercube coloring problem, Inform. Process. Lett. 84 (2002), 265-269.