Graph Theory

Number of Cliques in Minor-Closed Classes ★★

Author(s): Wood

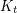Question   Is there a constant $ c $ such that every $ n $-vertex $ K_t $-minor-free graph has at most 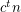$ c^tn $ cliques?

Keywords: clique; graph; minor

Posted by David Wood
updated October 12th, 2009
add new comment
Graph Theory » Graph Algorithms

A gold-grabbing game ★★

Author(s): Rosenfeld

Setup Fix a tree 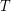$ T $ and for every vertex 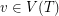$ v \in V(T) $ a non-negative integer 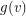$ g(v) $ which we think of as the amount of gold at $ v $.

2-Player game Players alternate turns. On each turn, a player chooses a leaf vertex $ v $ of the tree, takes the gold at this vertex, and then deletes $ v $. The game ends when the tree is empty, and the winner is the player who has accumulated the most gold.

Problem   Find optimal strategies for the players.

Keywords: game; tree

Posted by mdevos
updated October 4th, 2009
1 comment
Graph Theory » Topological G.T. » Crossing numbers

Crossing numbers and coloring ★★★

Author(s): Albertson

We let 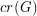$ cr(G) $ denote the crossing number of a graph $ G $.

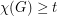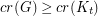Conjecture   Every graph $ G $ with $ \chi(G) \ge t $ satisfies $ cr(G) \ge cr(K_t) $.

Keywords: coloring; complete graph; crossing number

Posted by mdevos
updated September 4th, 2009
add new comment
Graph Theory » Basic G.T.

Domination in cubic graphs ★★

Author(s): Reed

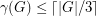Problem   Does every 3-connected cubic graph $ G $ satisfy $ \gamma(G) \le \lceil |G|/3 \rceil $ ?

Keywords: cubic graph; domination

Posted by mdevos
updated August 19th, 2009
add new comment
Unsorted

Do filters complementive to a given filter form a complete lattice? ★★

Author(s): Porton

Let 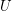$ U $ is a set. A filter (on 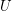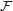$ U $) $ \mathcal{F} $ is by definition a non-empty set of subsets of 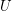$ U $ such that 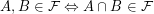$ A,B\in\mathcal{F} \Leftrightarrow A\cap B\in\mathcal{F} $. Note that unlike some other authors I do not require 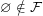$ \varnothing\notin\mathcal{F} $. I will denote 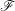$ \mathscr{F} $ the lattice of all filters (on 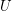$ U $) ordered by set inclusion.

Let 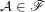$ \mathcal{A}\in\mathscr{F} $ is some (fixed) filter. Let 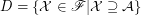$ D=\{\mathcal{X}\in\mathscr{F} | \mathcal{X}\supseteq \mathcal{A}\} $. Obviously 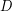$ D $ is a bounded lattice.

I will call complementive such filters 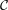$ \mathcal{C} $ that:

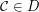  1. $ \mathcal{C}\in D $;
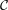  2. $ \mathcal{C} $ is a complemented element of the lattice $ D $.
Conjecture   The set of complementive filters ordered by inclusion is a complete lattice.

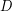Keywords: complete lattice; filter

Posted by porton
updated July 31st, 2009
add new comment