Open Problem Garden

Author(s): Goldberg

The overfull parameter is defined as follows: $w(G) = \max_{H \subseteq G} \left\lceil \frac{ |E(H)| }{ \lfloor \tfrac{1}{2} |V(H)| \rfloor} \right\rceil.$

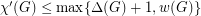Conjecture Every graph $G$ satisfies $\chi'(G) \le \max\{ \Delta(G) + 1, w(G) \}$ .

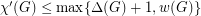Keywords: edge-coloring; multigraph

Posted by mdevos
updated June 5th, 2013

2 comments

r-graph

Graph Theory » Coloring » Edge coloring

Seymour's r-graph conjecture ★★★

Author(s): Seymour

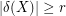An $r$ -graph is an $r$ -regular graph $G$ with the property that $|\delta(X)| \ge r$ for every 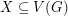$X \subseteq V(G)$ with odd size.

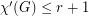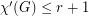Conjecture $\chi'(G) \le r+1$ for every $r$ -graph $G$ .

Keywords: edge-coloring; r-graph

Posted by mdevos
updated October 3rd, 2008

add new comment

Theoretical Comp. Sci. » Complexity

Discrete Logarithm Problem ★★★

Author(s):

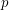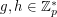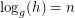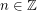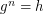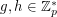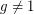If $p$ is prime and $g,h \in {\mathbb Z}_p^*$ , we write $\log_g(h) = n$ if $n \in {\mathbb Z}$ satisfies $g^n = h$ . The problem of finding such an integer $n$ for a given $g,h \in {\mathbb Z}^*_p$ (with $g \neq 1$ ) is the Discrete Log Problem.