 login/create account
login/create account
Seymour's r-graph conjecture
An  -graph is an
-graph is an  -regular graph
-regular graph  with the property that
with the property that 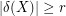 for every
for every 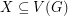 with odd size.
with odd size.
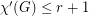 for every
for every  -graph
-graph  .
. This conjecture is among the most important unsolved problems in edge coloring. It is very close in nature to Goldberg's Conjecture, and is also closely related to Rizzi's packing postman sets conjecture (see packing T-joins).
If  is an
is an  -regular graph and there exists
-regular graph and there exists 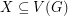 with
with 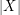 odd and
odd and 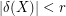 , then it is immediate that
, then it is immediate that  is not
is not  -edge-colourable, since every perfect matching must use at least one edge from
-edge-colourable, since every perfect matching must use at least one edge from 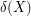 . This is in some sense the only obvious obstruction to
. This is in some sense the only obvious obstruction to  -edge-colorability that we know of. So,
-edge-colorability that we know of. So,  -graphs are the
-graphs are the  -regular graphs which do not fail to be
-regular graphs which do not fail to be  -edge-colorable for this obvious reason. Not every
-edge-colorable for this obvious reason. Not every  -graph is
-graph is  -edge-colorable, for instance Petersen's graph is a 3-graph which is not 3-edge-colorable. However, this conjecture asserts that all such graphs are still
-edge-colorable, for instance Petersen's graph is a 3-graph which is not 3-edge-colorable. However, this conjecture asserts that all such graphs are still 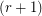 -edge-colorable.
-edge-colorable.
This conjecture has been proved for 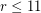 by Nishizeki and Kashiwagi [NK].
by Nishizeki and Kashiwagi [NK].
Bibliography
[NK] T. Nishizeki and K. Kashiwagi, An upper bound on the chromatic index of multigraphs. Graph theory with applications to algorithms and computer science (Kalamazoo, Mich., 1984), 595--604, Wiley-Intersci. Publ., Wiley, New York, 1985. MathSciNet.
*[S] P.D. Seymour, On multicolourings of cubic graphs, and conjectures of Fulkerson and Tutte. Proc. London Math. Soc. (3) 38 (1979), no. 3, 423--460. MathSciNet.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University