 login/create account
login/create account
Subgroup formed by elements of order dividing n ★★
Author(s): Frobenius
Conjecture
Suppose  is a finite group, and
is a finite group, and  is a positive integer dividing
is a positive integer dividing 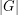 . Suppose that
. Suppose that  has exactly
has exactly  solutions to
solutions to 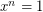 . Does it follow that these solutions form a subgroup of
. Does it follow that these solutions form a subgroup of  ?
?
Keywords: order, dividing
Seagull problem ★★★
Author(s): Seymour
Conjecture Every  vertex graph with no independent set of size
vertex graph with no independent set of size 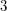 has a complete graph on
has a complete graph on 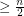 vertices as a minor.
vertices as a minor.
 vertex graph with no independent set of size
vertex graph with no independent set of size 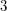 has a complete graph on
has a complete graph on 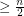 vertices as a minor.
vertices as a minor. Keywords: coloring; complete graph; minor
$C^r$ Stability Conjecture ★★★★
Conjecture Any 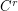 structurally stable diffeomorphism is hyperbolic.
structurally stable diffeomorphism is hyperbolic.
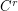 structurally stable diffeomorphism is hyperbolic.
structurally stable diffeomorphism is hyperbolic. Keywords: diffeomorphisms,; dynamical systems

 Drupal
Drupal CSI of Charles University
CSI of Charles University