A construction on boolean lattices is itself a boolean lattice? (Solved)

Importance: Medium ✭✭

Author(s):

Subject:

Keywords:	boolean algebra
	boolean lattice
	lattice

Recomm. for undergrads: no

Posted	by:	porton
	on:	October 12th, 2015

Solved by:

Porton, Victor

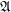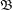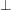Let $\mathfrak{A}$ and $\mathfrak{B}$ be (fixed) boolean lattices (with lattice operations denoted $\sqcup$ and $\sqcap$ , bottom element $\bot$ and top element $\top$ ).

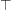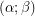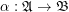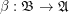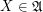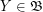I call a boolean funcoid a pair $(\alpha;\beta)$ of functions $\alpha:\mathfrak{A}\rightarrow\mathfrak{B}$ , $\beta:\mathfrak{B}\rightarrow\mathfrak{A}$ such that (for every $X\in\mathfrak{A}$ , $Y\in\mathfrak{B}$ ) $Y\sqcap^{\mathfrak{B}}\alpha(X)\ne\bot^{\mathfrak{B}} \Leftrightarrow X\sqcap^{\mathfrak{A}}\beta(Y)\ne\bot^{\mathfrak{A}}.$

(Boolean funcoids are a special case of pointfree funcoids as defined in my free ebook.)

Order boolean funcoids by the formula 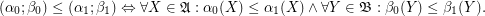$(\alpha_0;\beta_0)\le (\alpha_1;\beta_1) \Leftrightarrow \forall X\in\mathfrak{A}: \alpha_0(X)\le\alpha_1(X) \land \forall Y\in\mathfrak{B}: \beta_0(Y)\le\beta_1(Y).$

Conjecture The set of boolean funcoids with above defined order is itself a boolean lattice.

If this conjecture does not hold in general, does it hold for: a. atomic boolean lattices? b. atomistic boolean lattices? c. complete boolean lattices?

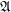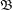For the special case when $\mathfrak{A}$ and $\mathfrak{B}$ are complete atomic boolean lattices, the conjecture easily follows from this math.SE answer.

See Algebraic General Topology for definitions of used concepts.

It is mostly solved:

Theorem Pointfree funcoids between a complete boolean lattice and an atomistic boolean lattice always form a boolean lattice.

Theorem Pointfree funcoids between a non-atomic boolean lattice and itself always do not form a boolean lattice.

It is not a complete answer, but the most important cases are considered. So I mark this question as solved. Further consideration however is welcome.