 login/create account
login/create account
Alexa's Conjecture on Primality
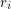 be the unique integer (with respect to a fixed
be the unique integer (with respect to a fixed 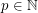 ) such that
) such that
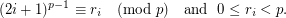
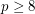 is a prime iff
is a prime iff ![$$ \displaystyle \sum_{i=1}^{\left \lfloor \frac{\sqrt[3]p}{2} \right \rfloor} r_i = \left \lfloor \frac{\sqrt[3]p}{2} \right \rfloor $$](/files/tex/99af565f4cc4d3bab11eb3fbf54f78626678d484.png)
The conjecture is obviously true when 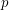 is prime, so it suffices to check when
is prime, so it suffices to check when 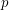 is composite.
is composite.
Bibliography
* indicates original appearance(s) of problem.
don't work either
your new statement is ambiguous (which r_i should one choose inside the sum?). I'm assuming you're just trying to move the "mod p" to apply to the sum only (and not to the RHS). If that's what you're doing, it still doesn't work. Same counter-examples at p=66, 102, 246 and 492 for p from 8 to 500.
donit work either
Yes it works .I have checked statement up to 10^6 ,there is no counterexample...
still ambiguous
then please re-word your conjecture, because as it stands, it's ambiguous and not true. It's ambiguous, because the way you defined r_i, one could have chosen r_i, r_i + p, r_i + 2p etc., but when you plug these into the sum, you get a different sum and the equality doesn't make sense.
still not good
your modified version now reduces back to putting mod p on the LHS of the equation, which as I've pointed out above, doesn't work (see counter-examples I gave). Where did you come up with this conjecture? Is there any published reference for it?
Fixed
I've corrected the statement on Alexa's behalf. This version holds up to at least 100 million.

 Drupal
Drupal CSI of Charles University
CSI of Charles University
counter-example for p=66
formula works for p from 8 through 100, except for p=66.