 login/create account
login/create account
Antichains in the cycle continuous order
If  ,
, are graphs, a function
are graphs, a function 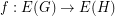 is called cycle-continuous if the pre-image of every element of the (binary) cycle space of
is called cycle-continuous if the pre-image of every element of the (binary) cycle space of  is a member of the cycle space of
is a member of the cycle space of  .
.
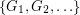 so that there is no cycle continuous mapping between
so that there is no cycle continuous mapping between 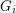 and
and 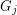 whenever
whenever 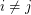 ?
? The definition of a cycle-continuous mapping is based on some work of Jaeger, and the most interesting question on this subject is undoubtedly Jaeger's Petersen coloring conjecture.
Let us define a relation on the set of all finite graphs with at least one edge by the rule 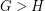 if there is a cycle-continuous mapping from
if there is a cycle-continuous mapping from  to
to  . It is not difficult to verify that
. It is not difficult to verify that 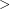 is a quasi order (reflexive and transitive). In this order, every Eulerian graph dominates every other graph, and every graph with a cut edge is dominated by every other graph.
is a quasi order (reflexive and transitive). In this order, every Eulerian graph dominates every other graph, and every graph with a cut edge is dominated by every other graph.
Let 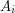 be the graph on two vertices with
be the graph on two vertices with 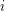 parallel edges. Then
parallel edges. Then  with all the inequalities strict, so this sequence is an infinite chain. Very little else seems to be known about this order. In particular, the problem highlighted above - does there exist an infinite antichain? remains open.
with all the inequalities strict, so this sequence is an infinite chain. Very little else seems to be known about this order. In particular, the problem highlighted above - does there exist an infinite antichain? remains open.
Bibliography
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University