Home » Subject » Graph Theory » Coloring

Total Colouring Conjecture

Importance: High ✭✭✭
Author(s): Behzad, M.
Subject: Graph Theory
» Coloring
Keywords: Total coloring
Recomm. for undergrads: no
Posted by: Iradmusa
on: June 4th, 2008
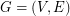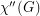Conjecture   A total coloring of a graph $ G = (V,E) $ is an assignment of colors to the vertices and the edges of $ G $ such that every pair of adjacent vertices, every pair of adjacent edges and every vertex and incident edge pair, receive different colors. The total chromatic number of a graph $ G $, $ \chi''(G) $, equals the minimum number of colors needed in a total coloring of $ G $. 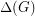It is an old conjecture of Behzad that for every graph $ G $, the total chromatic number equals the maximum degree of a vertex in $ G $, $ \Delta(G) $ plus one or two. In other words, \[\chi''(G)=\Delta(G)+1\ \ or \ \ \Delta(G)+2.\]

The lower bound 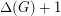$ \Delta(G)+1 $ is trivial by looking at the number of colours required on a vertex of maximum degree and its incident edges. It is easy to prove 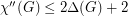$ \chi''(G)\leq 2\Delta(G)+2 $. Molloy and Reed [MR] showed that there exists a constant 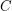$ C $ such that 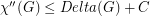$ \chi''(G)\leq Delta(G)+C $ for every graph $ G $.

The Edge list coloring conjecture would imply that 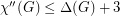$ \chi''(G)\leq \Delta(G)+3 $.

The Total Colouring Conjecture was proved for 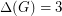$ \Delta(G)=3 $ by Rosenfeld [R] and also by Vijayaditya [V], and for 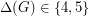$ \Delta(G)\in\{4,5\} $ by Kostochka [K1,K2,K3]; in fact the proof for 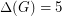$ \Delta(G)=5 $ holds for multigraphs.

The Conjecture has also been established for many graph classes. For every planar graph G with 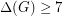$ \Delta(G) \geq 7 $, the following clever argument proves it. By the 4 Color Theorem, we can color the vertices with the colors 1, 2, 3, 4. By a result of Sanders and Zhao [SZ], we can color the edges of the graph with the colors 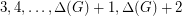$ 3, 4, \ldots, \Delta(G) + 1, \Delta(G) + 2 $. Uncolor each edge that was colored 3 or 4. Note that each uncolored edge has exactly two colors from 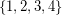$ \{1,2,3,4\} $ forbidden. Hence, each uncolored edge has at least two colors available. Note that the uncolored edges induce a disjoint union of paths and even cycles. Thus, by a special case of a theorem of Erdos, Rubin, and Taylor [ERT], we can color the edges from their lists of two available colors each.

Related problems

Edge list coloring conjecture
List Total Colouring Conjecture

Bibliography

*[B] M. Behzad, Graphs and their chromatic numbers, Ph.D. Thesis, Michigan State University, 1965.

[ERT] P. Erdos, A.L. Rubin, and H. Taylor, Choosability in graph, Cong. Numer. 26, 125-157, 1979.

[K1] A.V. Kostochka, The total coloring of a multigraph with maximal degree 4. Discrete Math. 17, 161-163, 1977.

[K2] A.V. Kostochka, Upper bounds of chromatic functions of graph (in Russian). Ph.D. Thesis, Novosibirsk, 1978.

[K3] A.V. Kostochka, Exact upper bound for the total chromatic number of a graph (in Russian). In: Proc. 24th Int. Wiss. Koll., Tech Hochsch. Ilmenau, 1979, pages 33-36, 1979.

[MR] M. Molloy and B.Reed. A bound on the total chromatic number. Combinatorica, 18(2), 241-280, 1998.

[R] M. Rosenfeld, On the total coloring of certain graphs. Israel J. Math. 9, 396-402, 1971.

[SZ] D.P. Sanders and Y. Zhao, Planar Graphs of Maximum Degree Seven are Class 1. J. Comb. Theory B. 83, 201-212, 2001.

[V] N. Vijayaditya, On total chormatic number of a graph. J. London Math. Soc. (2) 3, 405-408, 1971.


* indicates original appearance(s) of problem.
add new comment