 login/create account
login/create account
Circular coloring triangle-free subcubic planar graphs
Problem Does every triangle-free planar graph of maximum degree three have circular chromatic number at most 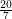 ?
?
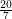 ?
? Throughout, we let 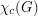 denote the circular chromatic number of the graph
denote the circular chromatic number of the graph  .
.
A well-known Question of Nesetril asks if 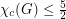 for all cubic graphs
for all cubic graphs  of sufficiently high girth. A conjecture of Jaeger asserts that
of sufficiently high girth. A conjecture of Jaeger asserts that 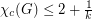 for every planar graph
for every planar graph  of girth
of girth 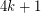 . There are numerous partial results on these problems, and there are many interesting questions concerning the circular chromatic numbers of restricted families of graphs. Here we are restricted to planar graphs of girth
. There are numerous partial results on these problems, and there are many interesting questions concerning the circular chromatic numbers of restricted families of graphs. Here we are restricted to planar graphs of girth 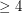 with maximum degree
with maximum degree 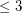 . The dodecahedron lives in this class and has
. The dodecahedron lives in this class and has 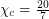 . It remains unclear if anyone else in this class might have
. It remains unclear if anyone else in this class might have 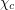 larger.
larger.
A related conjecture of X. Zhu asserts that for every triangle-free planar graph  with
with 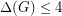 and
and 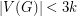 one has
one has 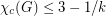 .
.
Bibliography
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University