Home » Subject » Graph Theory » Coloring » Vertex coloring

Colouring the square of a planar graph

Importance: Medium ✭✭
Author(s): Wegner
Subject: Graph Theory
» Coloring
» » Vertex coloring
Keywords:
Recomm. for undergrads: no
Posted by: fhavet
on: March 13th, 2013
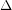Conjecture   Let $ G $ be a planar graph of maximum degree $ \Delta $. The chromatic number of its square is
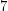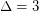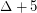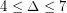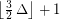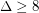    \item at most $ 7 $ if $ \Delta =3 $, \item at most $ \Delta+5 $ if $ 4\leq\Delta\leq 7 $, \item at most $ \left\lfloor\frac32\,\Delta\right\rfloor+1 $ if $ \Delta\ge8 $.

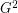The square of a graph $ G $ is the graph $ G^2 $ on the same set of vertices, in which two vertices are adjacent when their distance in $ G $ is at most 2.

Wegner [W] also gave examples showing that these bounds would be tight. For 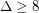$ \Delta\geq 8 $, they are the following.

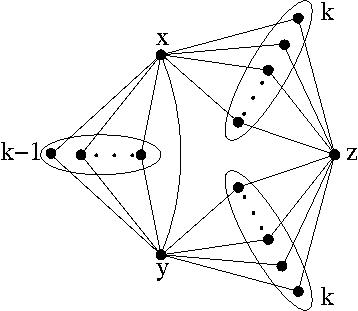
Tight examples for Wegner's conjecture

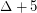For $ 4\leq \Delta \leq 9 $, the examples are planar graphs on $ \Delta+5 $ with maximum degree 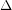$ \Delta $ whose square is a complete graph.

This conjecture has also been generalized to the list chromatic number.

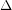Conjecture   Let $ G $ be a planar graph of maximum degree $ \Delta $. The list chromatic number of its square is
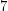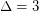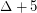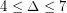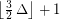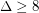    \item at most $ 7 $ if $ \Delta =3 $, \item at most $ \Delta+5 $ if $ 4\leq\Delta\leq 7 $, \item at most $ \left\lfloor\frac32\,\Delta\right\rfloor+1 $ if $ \Delta\ge8 $.

Cranston and Kim [CK] showed that the square of every connected graph (non necessarily planar) which is subcubic (i.e., with 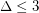$ \Delta\le3 $) is 8-choosable, except for the Petersen graph. However, the 7-choosability of the square of subcubic planar graphs is still open.

Havet et al. [HHMR] proved the conjecture asymptotically:

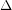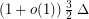Theorem   The square of every planar graph $ G $ of maximum degree $ \Delta $ has list chromatic number at most $ (1+o(1))\,\frac32\,\Delta $.

In fact, they proved this results for more general classes of graph. This led them to pose the following problem.

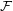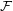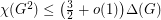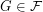Problem   Is it true that for every minor-closed family $ {\cal F} $ of graphs (with $ {\cal F} $ not the set of all graphs), we have $ \chi(G^2)\le \bigl(\frac32+o(1)\bigr) \Delta(G) $ for all $ G\in{\cal F} $?

Bibliography

[HHMR] F. Havet, J. van den Heuvel, C. McDiarmid, and B. Reed. List Colouring Squares of Planar Graphs. Research Report RR-6586, INRIA, July 2008.

[CK] D. W. Cranston and S.-J. Kim. List-coloring the square of a subcubic graph, J. Graph Theory, 57(1):65--87, 2008.

*[W] G. Wegner. Graphs with given diameter and a coloring problem. Technical report, 1977.


* indicates original appearance(s) of problem.
add new comment