 login/create account
login/create account
Laplacian Degrees of a Graph
 is a connected graph on
is a connected graph on  vertices, then
vertices, then 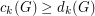 for
for 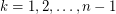 .
. (Reproduced from [M].)
Let  be the Laplacian matrix of a graph
be the Laplacian matrix of a graph  of order
of order  . Let
. Let 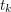 be the
be the  -th largest eigenvalue of
-th largest eigenvalue of  (
(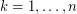 ). For the purpose of this problem, we call the number
). For the purpose of this problem, we call the number 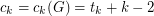 the
the  -th Laplacian degree of
-th Laplacian degree of  . In addition to that, let
. In addition to that, let 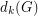 be the
be the  -th largest (usual) degree in
-th largest (usual) degree in  . It is known that every connected graph satisfies
. It is known that every connected graph satisfies 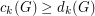 for
for 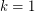 [GM],
[GM],  [LP] and for
[LP] and for 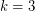 [G].
[G].
Bibliography
[GM] R. Grone, R. Merris, The Laplacian spectrum of a graph II, SIAM J. Discrete Math.7 (1994) 221-229. MathSciNet
[LP] J.S. Li, Y.L. Pan, A note on the second largest eigenvalue of the Laplacian matrix of a graph, Linear Multilin. Algebra 48 (2000) 117-121. MathSciNet
*[G] J.-M. Guo, On the third largest Laplacian eigenvalue of a graph, Linear Multilin. Algebra 55 (2007) 93-102. MathSciNet
[M] B. Mohar, Problem of the Month
* indicates original appearance(s) of problem.
Equality?
Any conjectures about the structure of the graphs for which equality holds (for any particular value of k)?
Gordon Royle

 Drupal
Drupal CSI of Charles University
CSI of Charles University
Proved
Proved by Willem Haemers and Andries Brouwer, see guo.pdf.