 login/create account
login/create account
Lovász Path Removal Conjecture
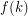 such that if
such that if  is any
is any 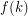 -connected graph and
-connected graph and  and
and 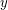 are any two vertices of
are any two vertices of  , then there exists an induced path
, then there exists an induced path 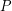 with ends
with ends  and
and 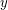 such that
such that 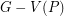 is
is  -connected.
-connected. It follows from a theorem of Tutte that any 3-connected graph contains a non-separating path connecting any two vertices, and consequently, 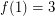 . When
. When 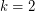 , it was independently shown by Chen, Gould, and Yu [CGY] and Kriesell [K] that
, it was independently shown by Chen, Gould, and Yu [CGY] and Kriesell [K] that 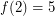 .
.
Anwering a conjecture of Kriesell, Kawarabayashi et al. [KLRW] proved the following weaker statement, in which one only removes the edges of the path.
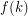 such that for every
such that for every 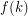 -connected graph
-connected graph  and any two vertices
and any two vertices  and
and 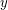 of
of  , there exists an induced path
, there exists an induced path 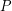 with ends
with ends  and
and 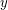 such that
such that 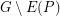 is
is  -connected.
-connected. Bibliography
[CGY] G. Chen, R. Gould, X. Yu, Graph connectivity after path removal, Combinatorica 23 (2003) 185--203.
[KLRW] K. Kawarabayashi, O. Lee, B. Reed, and P. Wollan, A weaker version of Lovasz's path removal conjecture, Journal of Combinatorial Theory, Series B 98 (2008) 972--979.
[K] M. Kriesell, Induced paths in 5-connected graphs, J. of Graph Theory, 36 (2001), 52--58.
*[T] C. Thomassen, Graph decompositions with applications to subdivisions and path systems modulo k, J. of Graph Theory, 7 (1983), 261--271.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University