 login/create account
login/create account
Rota's basis conjecture
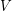 be a vector space of dimension
be a vector space of dimension  and let
and let 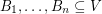 be bases. Then there exist
be bases. Then there exist  disjoint transversals of
disjoint transversals of 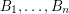 each of which is a base.
each of which is a base. This very pretty conjecture of Rota has a number of interesting extensions. One (obvious) extension is to matroids, and indeed, Rota conjectured this generalization (just replace the vector space  of dimension
of dimension  by a matroid
by a matroid 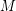 of rank
of rank  ). This generalization has received some recent attention: Geelen and Humphries [GH] proved the special case when
). This generalization has received some recent attention: Geelen and Humphries [GH] proved the special case when 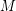 is a paving matroid, Geelen and Webb [GW] proved that in general there exist
is a paving matroid, Geelen and Webb [GW] proved that in general there exist 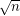 disjoint transversals which are bases, and Aharoni and Berger [AB] used their beautiful "intersection of a matroid and a simplicial complex" theorem to prove that the union of the bases can be partitioned into
disjoint transversals which are bases, and Aharoni and Berger [AB] used their beautiful "intersection of a matroid and a simplicial complex" theorem to prove that the union of the bases can be partitioned into  partial independent transversals. Another generalization of Rota's basis conjecture is the following.
partial independent transversals. Another generalization of Rota's basis conjecture is the following.
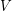 be a vector space of dimension
be a vector space of dimension  and for
and for 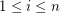 and
and 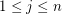 let
let 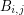 be a basis. Then we may choose a vector
be a basis. Then we may choose a vector 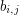 from each basis
from each basis 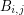 so that in the matrix
so that in the matrix 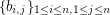 , every row and every column is a basis.
, every row and every column is a basis. To the best of my (M. DeVos') knowledge, this conjecture may generalize to matroids as well. There is another conjecture which implies Rota's basis conjecture which is far less obvious. In fact, Rota's conjecture (for even  and characteristic zero) is implied by Alon and Tarsi's Even vs. odd latin squares conjecture. This implication was first discovered by Rota and Huang [RH] (Rota had himself made another conjecture equivalent to that of Alon and Tarsi), and a very transparent proof of this fact based on a polynomial identity is given by Shmuel Onn [O].
and characteristic zero) is implied by Alon and Tarsi's Even vs. odd latin squares conjecture. This implication was first discovered by Rota and Huang [RH] (Rota had himself made another conjecture equivalent to that of Alon and Tarsi), and a very transparent proof of this fact based on a polynomial identity is given by Shmuel Onn [O].
Thanks to this last implication, partial results on the Alon-Tarsi conjecture show that Rota's basis conjecture holds whenever  has the form
has the form 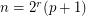 or
or 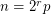 where
where 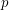 is an odd prime [D1], [D2], [Z].
is an odd prime [D1], [D2], [Z].
In August 2020, an asymptotic solution to the matroid's generalization of the conjecture was announced by Alexey Pokrovskiy [P].
Bibliography
[AB] R. Aharoni, E. Berger, The intersection of a matroid and a simplicial complex. Trans. Amer. Math. Soc. 358 (2006), no. 11, 4895--4917 MathSciNet.
[AT] N. Alon, M. Tarsi, Coloring and Orientations of Graphs. Combinatorica 12, 125-143, 1992 MathSciNet
[D1] A. Drisko, On the number of even and odd Latin squares of order 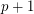 , Adv. Math. 128 (1997), no. 1, 20--35. MathSciNet
, Adv. Math. 128 (1997), no. 1, 20--35. MathSciNet
[D2] A. Drisko, Proof of the Alon-Tarsi conjecture for 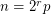 . Electron. J. Combin. 5 (1998) MathSciNet.
. Electron. J. Combin. 5 (1998) MathSciNet.
[GH] J. Geelen, and P. J. Humphries, Rota's basis conjecture for paving matroids. SIAM J. Discrete Math. 20 (2006), no. 4, 1042--1045 MathSciNet.
[GW] J. Geelen, and K. Webb, On Rota's basis conjecture
*[HR] R. Huang and G-C Rota, On the relations of various conjectures on Latin squares and straightening coefficients. Discrete Math. 128 (1994), no. 1-3, 225--236. MathSciNet.
[O] S. Onn, A colorful determinantal identity, a conjecture of Rota, and Latin squares. Amer. Math. Monthly 104 (1997), no. 2, 156--159. MathSciNet.
[P] A. Pokrovskiy, Rota’s Basis Conjecture holds asymptotically arXiv e-prints.
[W] M. Wild, On Rota's problem about  bases in a rank
bases in a rank  matroid. Adv. Math. 108 (1994), no. 2, 336--345. MathSciNet.
matroid. Adv. Math. 108 (1994), no. 2, 336--345. MathSciNet.
[Z] P. Zappa, The Cayley determinant of the determinant tensor and the Alon-Tarsi Conjecture, Adv. Appl. Math. 19 (1997), 31--44.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University
Rota's Basis Conjecture is still open
Dear Jon Noel, I believe that the following statement that you added to this posting on Aug. 28, 2013 is incorrect:
“It has been announced that Rota's Basis Conjecture has been proved by Geelen, Gerards and Whittle (2013). The proof reportedly applies a Theory of Matroid Minors developed by the authors.”
The announcement you referred to is actually regarding a different famous conjecture, called Rota’s conjecture, about forbidden minors of matroids. Besides the common author, the latter conjecture has nothing to do with Rota's Basis Conjecture which is, as far as I am concerned, still open.
Consequently I’m removing your statement and returning the status of the problem to unsolved.