Home » Subject » Theoretical Comp. Sci.

Sums of independent random variables with unbounded variance

Importance: Medium ✭✭
Author(s): Feige, Uriel
Subject: Theoretical Computer Science
Keywords: Inequality
Probability Theory
randomness in TCS
Recomm. for undergrads: no
Posted by: cwenner
on: April 2nd, 2009
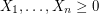Conjecture   If $ X_1, \dotsc, X_n \geq 0 $ are independent random variables with $ \mathbb{E}[X_i] \leq \mu $, then $$\mathrm{Pr} \left( \sum X_i - \mathbb{E} \left[ \sum X_i \right ] < \delta \mu \right) \geq \min \left ( (1 + \delta)^{-1} \delta, e^{-1} \right).$$

In comparison to most probabilistic inequalities (like Hoeffding's), Feige's inequality does not deteriorate as $ n $ goes to infinity, something that is useful for computer scientists.

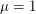Let $ T = \mathbb{E}\left [ \sum X_i \right ] + \delta $. Feige argued that to prove the conjecture, one only needs to prove it for the case when $ \mu = 1 $ and each variable 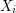$ X_i $ has the entire probability mass distributed on 0 and 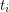$ t_i $ for some $ \mathbb{E}[X_i] \leq t_i \leq T $. He proved that $ \mathrm{Pr} \left( \sum X_i - \mathbb{E} \left[ \sum X_i \right ] < \delta \right) \geq \min \left ( (1 + \delta)^{-1} \delta, 1/13 \right), $ and conjectured that the constant 1/13 may be replaced with $ e^{-1} $. 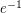It was further conjectured that "the worst case" would be one of

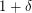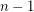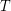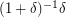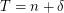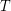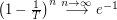    \item one variable has $ 1 + \delta $ as maximum value and the remaining $ n-1 $ random variables are always 1 (hence the probability that the sum is less than $ T $ is $ (1 + \delta)^{-1} \delta $), \item each variable has $ T = n + \delta $ as maximum (hence the probability that the sum is less than $ T $ is $ \left(1 - \frac{1}{T}\right)^n \stackrel{n \rightarrow \infty}{\longrightarrow} e^{-1} $).

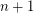One way to initiate an attack on this problem is to assume $ \delta = \mathbb{E}[X_i] = 1 $ and argue that the case when each variable assumes $ n + 1 $ with probability 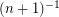$ (n+1)^{-1} $ and otherwise 0 is indeed the worst.

Bibliography

*[F04] Uriel Feige: On sums of independent random variables with unbounded variance, and estimating the average degree in a graph, STOC '04: Proceedings of the thirty-sixth annual ACM symposium on Theory of computing (2004), pp. 594 - 603. ACM

*[F05] Uriel Feige: On sums of independent random variables with unbounded variance, and estimating the average degree in a graph, Manuscript, 2005, [pdf]

The problem was also referenced at population algorithms, the blog.


* indicates original appearance(s) of problem.
add new comment