 login/create account
login/create account
Unsolvability of word problem for 2-knot complements
Problem Does there exist a smooth/PL embedding of 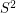 in
in 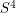 such that the fundamental group of the complement has an unsolvable word problem?
such that the fundamental group of the complement has an unsolvable word problem?
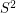 in
in 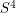 such that the fundamental group of the complement has an unsolvable word problem?
such that the fundamental group of the complement has an unsolvable word problem? It's known that there are smooth 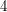 -dimensional submanifolds of
-dimensional submanifolds of 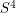 whose fundamental groups have unsolvable word problems. The complements of classical knots (
whose fundamental groups have unsolvable word problems. The complements of classical knots ( ) are known to have solvable word problems, as do arbitrary
) are known to have solvable word problems, as do arbitrary 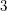 -manifold groups.
-manifold groups.
Bibliography
A. Dranisnikov, D. Repovs, "Embeddings up to homotopy type in Euclidean Space" Bull. Austral. Math. Soc (1993).
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University