 login/create account
login/create account
acyclic
Non-edges vs. feedback edge sets in digraphs ★★★
Author(s): Chudnovsky; Seymour; Sullivan
For any simple digraph  , we let
, we let 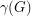 be the number of unordered pairs of nonadjacent vertices (i.e. the number of non-edges), and
be the number of unordered pairs of nonadjacent vertices (i.e. the number of non-edges), and 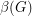 be the size of the smallest feedback edge set.
be the size of the smallest feedback edge set.
Conjecture If  is a simple digraph without directed cycles of length
is a simple digraph without directed cycles of length 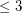 , then
, then 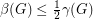 .
.
 is a simple digraph without directed cycles of length
is a simple digraph without directed cycles of length 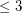 , then
, then 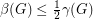 .
. Keywords: acyclic; digraph; feedback edge set; triangle free
The Two Color Conjecture ★★
Author(s): Neumann-Lara
Conjecture If  is an orientation of a simple planar graph, then there is a partition of
is an orientation of a simple planar graph, then there is a partition of 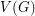 into
into 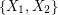 so that the graph induced by
so that the graph induced by 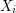 is acyclic for
is acyclic for 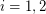 .
.
 is an orientation of a simple planar graph, then there is a partition of
is an orientation of a simple planar graph, then there is a partition of 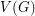 into
into 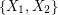 so that the graph induced by
so that the graph induced by 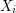 is acyclic for
is acyclic for 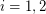 .
. 
 Drupal
Drupal CSI of Charles University
CSI of Charles University