 login/create account
login/create account
counting quantifiers
Vertex Cover Integrality Gap ★★
Author(s): Atserias
Conjecture For every 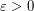 there is
there is 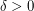 such that, for every large
such that, for every large  , there are
, there are  -vertex graphs
-vertex graphs  and
and 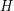 such that
such that  and
and 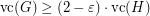 .
.
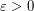 there is
there is 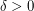 such that, for every large
such that, for every large  , there are
, there are  -vertex graphs
-vertex graphs  and
and 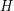 such that
such that  and
and 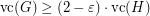 .
. Keywords: counting quantifiers; FMT12-LesHouches
Fixed-point logic with counting ★★
Author(s): Blass
Question Can either of the following be expressed in fixed-point logic plus counting:
- \item Given a graph, does it have a perfect matching, i.e., a set
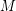 of edges such that every vertex is incident to exactly one edge from
of edges such that every vertex is incident to exactly one edge from 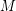 ? \item Given a square matrix over a finite field (regarded as a structure in the natural way, as described in [BGS02]), what is its determinant?
? \item Given a square matrix over a finite field (regarded as a structure in the natural way, as described in [BGS02]), what is its determinant? Keywords: Capturing PTime; counting quantifiers; Fixed-point logic; FMT03-Bedlewo

 Drupal
Drupal CSI of Charles University
CSI of Charles University