 login/create account
login/create account
Fixed-point logic with counting
Question Can either of the following be expressed in fixed-point logic plus counting:
- \item Given a graph, does it have a perfect matching, i.e., a set
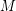 of edges such that every vertex is incident to exactly one edge from
of edges such that every vertex is incident to exactly one edge from 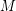 ? \item Given a square matrix over a finite field (regarded as a structure in the natural way, as described in [BGS02]), what is its determinant?
? \item Given a square matrix over a finite field (regarded as a structure in the natural way, as described in [BGS02]), what is its determinant? It is known that (1) is expressible if restricted to bipartite graphs and that (2) is expressible if the field has only two elements. Both these results are in [BGS02].
Bibliography
[BGS02] A. Blass, Y. Gurevich, and S. Shelah, On polynomial time computation over unordered structures, J. Symbolic Logic 67 (2002) 1093--1125.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University