Home » Author index

Erdos, Paul


Graph Theory » Directed Graphs » Tournaments

Monochromatic reachability in edge-colored tournaments ★★★

Author(s): Erdos

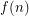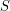Problem   For every $ n $, is there a (least) positive integer $ f(n) $ so that whenever a tournament has its edges colored with $ n $ colors, there exists a set $ S $ of at most 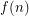$ f(n) $ vertices so that every vertex has a monochromatic path to some point in $ S $?

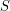Keywords: digraph; edge-coloring; tournament

Posted by mdevos
updated July 9th, 2008
add new comment
Number Theory » Combinatorial N.T.

Covering systems with big moduli ★★

Author(s): Erdos; Selfridge

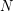Problem   Does for every integer $ N $ exist a covering system with all moduli distinct and at least equal to~$ N $?

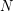Keywords: covering system

Posted by Robert Samal
updated August 4th, 2007
add new comment
Number Theory » Combinatorial N.T.

Odd incongruent covering systems ★★★

Author(s): Erdos; Selfridge

Conjecture   There is no covering system whose moduli are odd, distinct, and greater than 1.

Keywords: covering system

Posted by Robert Samal
updated August 4th, 2007
add new comment
Number Theory » Combinatorial N.T.

Sets with distinct subset sums ★★★

Author(s): Erdos

Say that a set 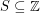$ S \subseteq {\mathbb Z} $ has distinct subset sums if distinct subsets of 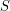$ S $ have distinct sums.

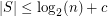Conjecture   There exists a fixed constant $ c $ so that $ |S| \le \log_2(n) + c $ whenever 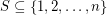$ S \subseteq \{1,2,\ldots,n\} $ has distinct subset sums.

Keywords: subset sum

Posted by mdevos
updated April 7th, 2011
1 comment
Number Theory » Additive N.T.

The Erdos-Turan conjecture on additive bases ★★★★

Author(s): Erdos; Turan

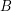Let $ B \subseteq {\mathbb N} $. The representation function $ r_B : {\mathbb N} \rightarrow {\mathbb N} $ for $ B $ is given by the rule 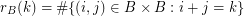$ r_B(k) = \#\{ (i,j) \in B \times B : i + j = k \} $. We call 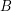$ B $ an additive basis if 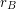$ r_B $ is never $ 0 $.

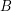Conjecture   If $ B $ is an additive basis, then 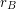$ r_B $ is unbounded.

Keywords: additive basis; representation function

Posted by mdevos
updated June 8th, 2007
add new comment
Combinatorics » Ramsey Theory

Diagonal Ramsey numbers ★★★★

Author(s): Erdos

Let 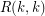$ R(k,k) $ denote the 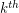$ k^{th} $ diagonal Ramsey number.

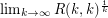Conjecture   $ \lim_{k \rightarrow \infty} R(k,k) ^{\frac{1}{k}} $ exists.
Problem   Determine the limit in the above conjecture (assuming it exists).

Keywords: Ramsey number

Posted by mdevos
updated September 13th, 2010
2 comments
Graph Theory » Infinite Graphs

Unions of triangle free graphs ★★★

Author(s): Erdos; Hajnal

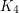Problem   Does there exist a graph with no subgraph isomorphic to $ K_4 $ which cannot be expressed as a union of 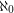$ \aleph_0 $ triangle free graphs?

Keywords: forbidden subgraph; infinite graph; triangle free

Posted by mdevos
updated June 4th, 2007
add new comment
Graph Theory » Topological G.T. » Crossing numbers

The Crossing Number of the Hypercube ★★

Author(s): Erdos; Guy

The crossing number 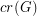$ cr(G) $ of $ G $ is the minimum number of crossings in all drawings of $ G $ in the plane.

The 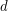$ d $-dimensional (hyper)cube 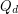$ Q_d $ is the graph whose vertices are all binary sequences of length 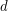$ d $, and two of the sequences are adjacent in 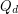$ Q_d $ if they differ in precisely one coordinate.

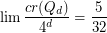
Conjecture   $ \displaystyle \lim \frac{cr(Q_d)}{4^d} = \frac{5}{32} $

Keywords: crossing number; hypercube

Posted by Robert Samal
updated July 18th, 2008
1 comment
Graph Theory » Extremal G.T.

The Erdös-Hajnal Conjecture ★★★

Author(s): Erdos; Hajnal

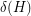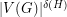Conjecture   For every fixed graph $ H $, there exists a constant $ \delta(H) $, so that every graph $ G $ without an induced subgraph isomorphic to $ H $ contains either a clique or an independent set of size $ |V(G)|^{\delta(H)} $.

Keywords: induced subgraph

Posted by mdevos
updated March 18th, 2007
add new comment
Syndicate content