 login/create account
login/create account
representation function
The Erdos-Turan conjecture on additive bases ★★★★
Let  . The representation function
. The representation function  for
for 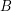 is given by the rule
is given by the rule 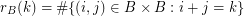 . We call
. We call 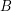 an additive basis if
an additive basis if 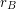 is never
is never  .
.
Conjecture If 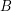 is an additive basis, then
is an additive basis, then 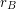 is unbounded.
is unbounded.
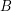 is an additive basis, then
is an additive basis, then 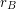 is unbounded.
is unbounded. Keywords: additive basis; representation function

 Drupal
Drupal CSI of Charles University
CSI of Charles University