 login/create account
login/create account
Porton, Victor
Upgrading a multifuncoid ★★
Author(s): Porton
Let 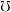 be a set,
be a set, 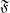 be the set of filters on
be the set of filters on 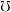 ordered reverse to set-theoretic inclusion,
ordered reverse to set-theoretic inclusion, 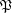 be the set of principal filters on
be the set of principal filters on 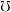 , let
, let  be an index set. Consider the filtrator
be an index set. Consider the filtrator 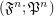 .
.
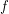 is a multifuncoid of the form
is a multifuncoid of the form 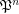 , then
, then 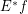 is a multifuncoid of the form
is a multifuncoid of the form 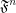 .
. See below for definition of all concepts and symbols used to in this conjecture.
Refer to this Web site for the theory which I now attempt to generalize.
Keywords:
Strict inequalities for products of filters ★
Author(s): Porton
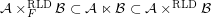 for some filter objects
for some filter objects 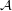 ,
, 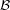 . Particularly, is this formula true for
. Particularly, is this formula true for 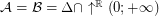 ?
? A weaker conjecture:
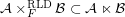 for some filter objects
for some filter objects 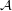 ,
, 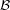 .
. Keywords: filter products
Join of oblique products ★★
Author(s): Porton
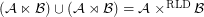 for every filter objects
for every filter objects 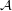 ,
, 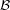 .
. Keywords: filter; oblique product; reloidal product
Outer reloid of restricted funcoid ★★
Author(s): Porton
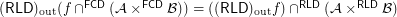 for every filter objects
for every filter objects  and
and  and a funcoid
and a funcoid 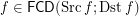 ?
? Keywords: direct product of filters; outer reloid
Characterization of monovalued reloids with atomic domains ★★
Author(s): Porton
- an injective reloid;
- a restriction of a constant function
(or both).
Keywords: injective reloid; monovalued reloid
Composition of reloids expressed through atomic reloids ★★
Author(s): Porton
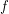 and
and 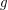 are composable reloids, then
are composable reloids, then 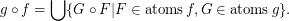
Keywords: atomic reloids
Outer reloid of direct product of filters ★★
Author(s): Porton
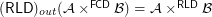 for every f.o.
for every f.o. 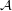 ,
, 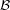 ?
? Keywords: direct product of filters; outer reloid
Chain-meet-closed sets ★★
Author(s): Porton
Let 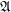 is a complete lattice. I will call a filter base a nonempty subset
is a complete lattice. I will call a filter base a nonempty subset 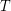 of
of 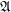 such that
such that 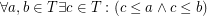 .
.
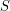 of a complete lattice
of a complete lattice 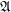 is chain-meet-closed iff for every non-empty chain
is chain-meet-closed iff for every non-empty chain 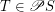 we have
we have 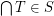 .
. 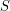 of a complete lattice
of a complete lattice 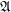 is chain-meet-closed iff for every filter base
is chain-meet-closed iff for every filter base 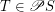 we have
we have 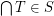 .
. Keywords: chain; complete lattice; filter bases; filters; linear order; total order
Co-separability of filter objects ★★
Author(s): Porton
 and
and  are filters on a set
are filters on a set 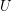 and
and 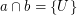 . Then
. Then 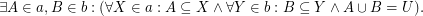
See here for some equivalent reformulations of this problem.
This problem (in fact, a little more general version of a problem equivalent to this problem) was solved by the problem author. See here for the solution.
Maybe this problem should be moved to "second-tier" because its solution is simple.
Keywords: filters

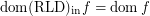 and
and 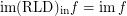 for every funcoid
for every funcoid  Drupal
Drupal CSI of Charles University
CSI of Charles University