 login/create account
login/create account
Porton, Victor
Pseudodifference of filter objects ★★
Author(s): Porton
Let 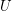 is a set. A filter
is a set. A filter 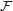 (on
(on 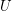 ) is a non-empty set of subsets of
) is a non-empty set of subsets of 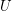 such that
such that 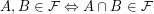 . Note that unlike some other authors I do not require
. Note that unlike some other authors I do not require 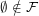 .
.
I will call the set of filter objects the set of filters ordered reverse to set theoretic inclusion of filters, with principal filters equated to the corresponding sets. See here for the formal definition of filter objects. I will denote 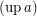 the filter corresponding to a filter object
the filter corresponding to a filter object  . I will denote the set of filter objects (on
. I will denote the set of filter objects (on 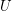 ) as
) as 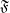 .
.
I will denote  the set of atomic lattice elements under a given lattice element
the set of atomic lattice elements under a given lattice element  . If
. If  is a filter object, then
is a filter object, then  is essentially the set of ultrafilters over
is essentially the set of ultrafilters over  .
.
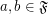 for each set
for each set 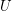 ? (If some are not equal, provide counter-examples.)
? (If some are not equal, provide counter-examples.)- \item
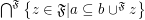 ;
;
\item 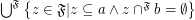 ;
;
\item 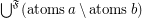 ;
;
\item 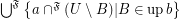 .
.
Keywords: filters; pseudodifference
Do filters complementive to a given filter form a complete lattice? ★★
Author(s): Porton
Let 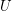 is a set. A filter (on
is a set. A filter (on 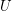 )
) 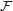 is by definition a non-empty set of subsets of
is by definition a non-empty set of subsets of 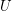 such that
such that 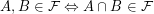 . Note that unlike some other authors I do not require
. Note that unlike some other authors I do not require 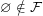 . I will denote
. I will denote 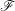 the lattice of all filters (on
the lattice of all filters (on 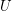 ) ordered by set inclusion.
) ordered by set inclusion.
Let 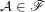 is some (fixed) filter. Let
is some (fixed) filter. Let 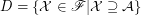 . Obviously
. Obviously 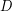 is a bounded lattice.
is a bounded lattice.
I will call complementive such filters 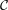 that:
that:
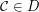 ;
;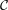 is a complemented element of the lattice
is a complemented element of the lattice 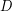 .
.
Keywords: complete lattice; filter
Monovalued reloid restricted to atomic filter ★★
Author(s): Porton
Weaker conjecture:
Keywords: monovalued reloid
Atomic reloids are monovalued ★★
Author(s): Porton
Keywords: atomic reloid; monovalued reloid; reloid
Composition of atomic reloids ★★
Author(s): Porton
Keywords: atomic reloid; reloid
Reloid corresponding to funcoid is between outward and inward reloid ★★
Author(s): Porton
Keywords: funcoid; inward reloid; outward reloid; reloid
Distributivity of union of funcoids corresponding to reloids ★★
Author(s): Porton
Keywords: funcoid; infinite distributivity; reloid
Inward reloid corresponding to a funcoid corresponding to convex reloid ★★
Author(s): Porton
Keywords: convex reloid; funcoid; functor; inward reloid; reloid
Outward reloid corresponding to a funcoid corresponding to convex reloid ★★
Author(s): Porton
Keywords: convex reloid; funcoid; functor; outward reloid; reloid

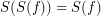 for every endo-
for every endo-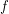 ?
? 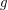 having the same source and destination
having the same source and destination ![\[ ( \mathsf{\tmop{RLD}})_{\tmop{out}} f \subseteq g \subseteq ( \mathsf{\tmop{RLD}})_{\tmop{in}} f \Leftrightarrow ( \mathsf{\tmop{FCD}}) g = f. \]](/files/tex/def032a20d7d57db67d77c0f002f1c9f2909fe98.png)
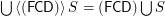 if
if 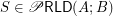 is a set of
is a set of 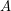 to a set
to a set 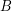 .
. 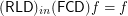 for any
for any 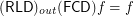 for any
for any  Drupal
Drupal CSI of Charles University
CSI of Charles University