 login/create account
login/create account
Porton, Victor
A construction of direct product in the category of continuous maps between endo-funcoids ★★★
Author(s): Porton
Consider the category of (proximally) continuous maps (entirely defined monovalued functions) between endo-funcoids.
Remind from my book that morphisms 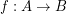 of this category are defined by the formula
of this category are defined by the formula 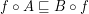 (here and below by abuse of notation I equate functions with corresponding principal funcoids).
(here and below by abuse of notation I equate functions with corresponding principal funcoids).
Let 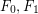 are endofuncoids,
are endofuncoids,
We define 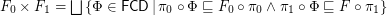
(here  and
and 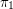 are cartesian projections).
are cartesian projections).
Keywords: categorical product; direct product
Distributivity of a lattice of funcoids is not provable without axiom of choice ★
Author(s): Porton
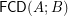 of funcoids (for arbitrary sets
of funcoids (for arbitrary sets  and
and 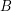 ) is not provable in ZF (without axiom of choice).
) is not provable in ZF (without axiom of choice). A similar conjecture:
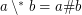 for arbitrary filters
for arbitrary filters  and
and  on a powerset cannot be proved in ZF (without axiom of choice).
on a powerset cannot be proved in ZF (without axiom of choice). Keywords: axiom of choice; distributive lattice; distributivity; funcoid; reverse math; reverse mathematics; ZF; ZFC
Values of a multifuncoid on atoms ★★
Author(s): Porton
![$ L \in \mathrel{\left[ f \right]} \Rightarrow \mathrel{\left[ f \right]} \cap \prod_{i \in \operatorname{dom} \mathfrak{A}} \operatorname{atoms} L_i \neq \emptyset $](/files/tex/20328c795890b2a043f28afc705aecd5679f72d9.png) for every multifuncoid
for every multifuncoid 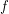 of the form whose elements are atomic posets.
of the form whose elements are atomic posets. Keywords:
A conjecture about direct product of funcoids ★★
Author(s): Porton
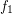 and
and 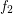 are monovalued, entirely defined funcoids with
are monovalued, entirely defined funcoids with 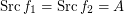 . Then there exists a pointfree funcoid
. Then there exists a pointfree funcoid 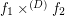 such that (for every filter
such that (for every filter  on
on  )
) 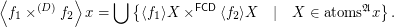 (The join operation is taken on the lattice of filters with reversed order.)
(The join operation is taken on the lattice of filters with reversed order.) A positive solution of this problem may open a way to prove that some funcoids-related categories are cartesian closed.
Keywords: category theory; general topology
Graph product of multifuncoids ★★
Author(s): Porton
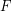 is a family of multifuncoids such that each
is a family of multifuncoids such that each 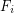 is of the form
is of the form 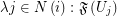 where
where 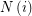 is an index set for every
is an index set for every 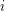 and
and 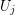 is a set for every
is a set for every 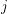 . Let every
. Let every 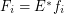 for some multifuncoid
for some multifuncoid 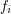 of the form
of the form 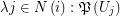 regarding the filtrator
regarding the filtrator 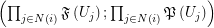 . Let
. Let  is a graph-composition of
is a graph-composition of 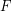 (regarding some partition
(regarding some partition  and external set
and external set 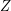 ). Then there exist a multifuncoid
). Then there exist a multifuncoid 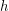 of the form
of the form 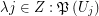 such that
such that 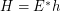 regarding the filtrator
regarding the filtrator 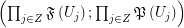 .
. Keywords: graph-product; multifuncoid
Atomicity of the poset of multifuncoids ★★
Author(s): Porton
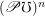 is for every sets
is for every sets 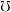 and
and  :
:- \item atomic; \item atomistic.
See below for definition of all concepts and symbols used to in this conjecture.
Refer to this Web site for the theory which I now attempt to generalize.
Keywords: multifuncoid
Atomicity of the poset of completary multifuncoids ★★
Author(s): Porton
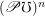 is for every sets
is for every sets 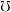 and
and  :
:- \item atomic; \item atomistic.
See below for definition of all concepts and symbols used to in this conjecture.
Refer to this Web site for the theory which I now attempt to generalize.
Keywords: multifuncoid
Upgrading a completary multifuncoid ★★
Author(s): Porton
Let 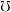 be a set,
be a set, 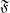 be the set of filters on
be the set of filters on 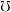 ordered reverse to set-theoretic inclusion,
ordered reverse to set-theoretic inclusion, 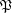 be the set of principal filters on
be the set of principal filters on 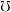 , let
, let  be an index set. Consider the filtrator
be an index set. Consider the filtrator 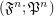 .
.
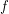 is a completary multifuncoid of the form
is a completary multifuncoid of the form 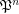 , then
, then 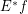 is a completary multifuncoid of the form
is a completary multifuncoid of the form 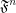 .
. See below for definition of all concepts and symbols used to in this conjecture.
Refer to this Web site for the theory which I now attempt to generalize.
Keywords:
Funcoidal products inside an inward reloid ★★
Author(s): Porton
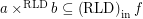 then
then 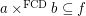 for every funcoid
for every funcoid 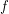 and atomic f.o.
and atomic f.o.  and
and  on the source and destination of
on the source and destination of 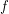 correspondingly.
correspondingly. A stronger conjecture:
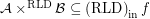 then
then 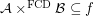 for every funcoid
for every funcoid 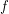 and
and 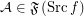 ,
, 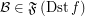 .
. Keywords: inward reloid
Distributivity of inward reloid over composition of funcoids ★★
Author(s): Porton
Keywords: distributive; distributivity; funcoid; functor; inward reloid; reloid

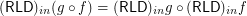 for any composable
for any composable 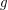 .
.  Drupal
Drupal CSI of Charles University
CSI of Charles University