Home » Subject » Graph Theory » Coloring » Homomorphisms
Importance: Medium ✭✭
Author(s): Fomin, Fedor V.
Heggernes, Pinar
Kratsch, Dieter
Subject: Graph Theory
» Coloring
» » Homomorphisms
Keywords: algorithm
Exponential-time algorithm
homomorphism
Recomm. for undergrads: no
Posted by: jfoniok
on: July 8th, 2010
Question  

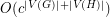Is there an algorithm that decides, for input graphs $ G $ and $ H $, whether there exists a homomorphism from $ G $ to $ H $ in time $ O(c^{|V(G)|+|V(H)|}) $ for some constant $ c $?

An affirmative answer is known in several cases: if 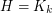$ H=K_k $ (graph coloring) [L], [BH], [K]; if $ H $ has bounded treewidth [FHK]; if $ H $ has bounded cliquewidth [W].

Bibliography

[BH] Andreas Björklund, Thore Husfeldt: Inclusion--Exclusion Algorithms for Counting Set Partitions, Proc. FOCS'06 (2006).

*[FHK] Fedor V. Fomin, Pinar Heggernes, Dieter Kratsch: Exact Algorithms for Graph Homomorphisms, Theory Comput. Syst. 41 (2007), no. 2, 381--393. MathSciNet

[K] Mikko Koivisto: An 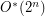$ O^\ast(2^n) $ Algorithm for Graph Coloring and Other Partitioning Problems via Inclusion--Exclusion, Proc. FOCS'06 (2006).

[L] Eugene L. Lawler: A note on the complexity of the chromatic number problem, Information Processing Lett. 5 (1976), no. 3, 66--67. MathSciNet

[W] Magnus Wahlström: New Plain-Exponential Time Classs for Graph Homomorphism, CSR2009, LNCS5675 (2009), 346--355.


* indicates original appearance(s) of problem.
add new comment

Reply

Comments are limited to a maximum of 1000 characters.
More information about formatting options