 login/create account
login/create account
homomorphism
Sidorenko's Conjecture ★★★
Author(s): Sidorenko
 and graph
and graph  , the number of homomorphisms from
, the number of homomorphisms from  to
to  is at least
is at least 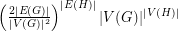 .
. Keywords: density problems; extremal combinatorics; homomorphism
Algorithm for graph homomorphisms ★★
Author(s): Fomin; Heggernes; Kratsch
Is there an algorithm that decides, for input graphs  and
and  , whether there exists a homomorphism from
, whether there exists a homomorphism from  to
to  in time
in time 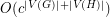 for some constant
for some constant  ?
?
Keywords: algorithm; Exponential-time algorithm; homomorphism
Hedetniemi's Conjecture ★★★
Author(s): Hedetniemi
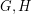 are simple finite graphs, then
are simple finite graphs, then  .
. Here 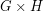 is the tensor product (also called the direct or categorical product) of
is the tensor product (also called the direct or categorical product) of  and
and  .
.
Keywords: categorical product; coloring; homomorphism; tensor product
Weak pentagon problem ★★
Author(s): Samal
 is a cubic graph not containing a triangle, then it is possible to color the edges of
is a cubic graph not containing a triangle, then it is possible to color the edges of  by five colors, so that the complement of every color class is a bipartite graph.
by five colors, so that the complement of every color class is a bipartite graph. Keywords: Clebsch graph; cut-continuous mapping; edge-coloring; homomorphism; pentagon
Mapping planar graphs to odd cycles ★★★
Author(s): Jaeger
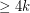 has a homomorphism to
has a homomorphism to 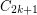 .
. Keywords: girth; homomorphism; planar graph
Pentagon problem ★★★
Author(s): Nesetril
 be a 3-regular graph that contains no cycle of length shorter than
be a 3-regular graph that contains no cycle of length shorter than 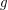 . Is it true that for large enough~
. Is it true that for large enough~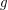 there is a homomorphism
there is a homomorphism 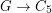 ?
? Keywords: cubic; homomorphism
A homomorphism problem for flows ★★
Author(s): DeVos
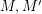 be abelian groups and let
be abelian groups and let 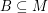 and
and 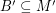 satisfy
satisfy 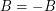 and
and 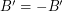 . If there is a homomorphism from
. If there is a homomorphism from 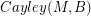 to
to 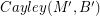 , then every graph with a B-flow has a B'-flow.
, then every graph with a B-flow has a B'-flow. Keywords: homomorphism; nowhere-zero flow; tension

 Drupal
Drupal CSI of Charles University
CSI of Charles University