 login/create account
login/create account
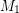 ,
, 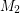 so that
so that 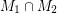 does not contain an odd edge-cut.
does not contain an odd edge-cut. Let 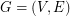 be a bridgeless cubic graph. A binary cycle (henceforth called cycle) is a set
be a bridgeless cubic graph. A binary cycle (henceforth called cycle) is a set 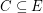 so that every vertex of
so that every vertex of 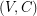 has even degree (equivalently, a cycle is any member of the binary cycle space). A postman join is a set
has even degree (equivalently, a cycle is any member of the binary cycle space). A postman join is a set 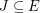 so that
so that 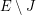 is a cycle. Note that since
is a cycle. Note that since  is cubic, every perfect matching is a postman join. Next we state a well-known theorem of Jaeger in three equivalent forms.
is cubic, every perfect matching is a postman join. Next we state a well-known theorem of Jaeger in three equivalent forms.
- \item
 has a nowhere-zero flow in the group
has a nowhere-zero flow in the group 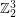 . \item
. \item  has three cycles
has three cycles 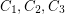 so that
so that 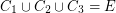 . \item
. \item  has three postman joins
has three postman joins 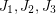 so that
so that 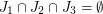 .
. The last of these statements is interesting, since The Berge Fulkerson Conjecture (if true) implies the following:
 has three perfect matchings
has three perfect matchings 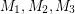 so that
so that 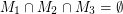 .
. So, we know that  has three postman joins
has three postman joins 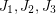 with empty intersection, and it is conjectured that
with empty intersection, and it is conjectured that 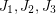 may be chosen so that each is a perfect matching, but now we see two statements in between the theorem and the conjecture. Namely, is it true that
may be chosen so that each is a perfect matching, but now we see two statements in between the theorem and the conjecture. Namely, is it true that 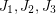 may be chosen so that one is a perfect matching? or two? The first of these was solved recently.
may be chosen so that one is a perfect matching? or two? The first of these was solved recently.
 has two postman sets
has two postman sets 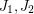 and one perfect matching
and one perfect matching 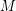 so that
so that 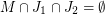
The second of these asks for two perfect matchings 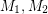 and one postman join
and one postman join 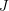 so that
so that 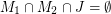 . It is an easy exercise to show that a set
. It is an easy exercise to show that a set 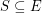 contains a postman join if an only if
contains a postman join if an only if 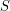 has nonempty intersection with every odd edge-cut. Therefore, finding two perfect matchings and one postman join with empty common intersection is precisely equivalent to the conjecture at the start of this page - find two perfect matchings whose intersection contains no odd edge-cut.
has nonempty intersection with every odd edge-cut. Therefore, finding two perfect matchings and one postman join with empty common intersection is precisely equivalent to the conjecture at the start of this page - find two perfect matchings whose intersection contains no odd edge-cut.
Bibliography
* Edita Macajova, Martin Skoviera, Fano colourings of cubic graphs and the Fulkerson conjecture. Theoret. Comput. Sci. 349 (2005), no. 1, 112--120. MathSciNet
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University