 login/create account
login/create account
nowhere-zero flow
The intersection of two perfect matchings ★★
Conjecture Every bridgeless cubic graph has two perfect matchings 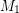 ,
, 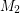 so that
so that 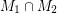 does not contain an odd edge-cut.
does not contain an odd edge-cut.
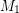 ,
, 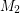 so that
so that 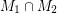 does not contain an odd edge-cut.
does not contain an odd edge-cut. Keywords: cubic; nowhere-zero flow; perfect matching
Half-integral flow polynomial values ★★
Author(s): Mohar
Let 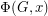 be the flow polynomial of a graph
be the flow polynomial of a graph  . So for every positive integer
. So for every positive integer  , the value
, the value 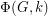 equals the number of nowhere-zero
equals the number of nowhere-zero  -flows in
-flows in  .
.
Conjecture  for every 2-edge-connected graph
for every 2-edge-connected graph  .
.
 for every 2-edge-connected graph
for every 2-edge-connected graph  .
. Keywords: nowhere-zero flow
A nowhere-zero point in a linear mapping ★★★
Author(s): Jaeger
Conjecture If 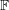 is a finite field with at least 4 elements and
is a finite field with at least 4 elements and  is an invertible
is an invertible 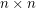 matrix with entries in
matrix with entries in 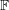 , then there are column vectors
, then there are column vectors 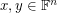 which have no coordinates equal to zero such that
which have no coordinates equal to zero such that 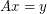 .
.
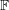 is a finite field with at least 4 elements and
is a finite field with at least 4 elements and  is an invertible
is an invertible 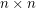 matrix with entries in
matrix with entries in 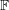 , then there are column vectors
, then there are column vectors 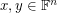 which have no coordinates equal to zero such that
which have no coordinates equal to zero such that 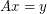 .
. Keywords: invertible; nowhere-zero flow
Unit vector flows ★★
Author(s): Jain
Conjecture There exists a map 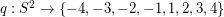 so that antipodal points of
so that antipodal points of 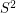 receive opposite values, and so that any three points which are equidistant on a great circle have values which sum to zero.
receive opposite values, and so that any three points which are equidistant on a great circle have values which sum to zero.
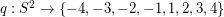 so that antipodal points of
so that antipodal points of  receive opposite values, and so that any three points which are equidistant on a great circle have values which sum to zero.
receive opposite values, and so that any three points which are equidistant on a great circle have values which sum to zero. Keywords: nowhere-zero flow
Real roots of the flow polynomial ★★
Author(s): Welsh
Conjecture All real roots of nonzero flow polynomials are at most 4.
Keywords: flow polynomial; nowhere-zero flow
A homomorphism problem for flows ★★
Author(s): DeVos
Conjecture Let 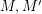 be abelian groups and let
be abelian groups and let  and
and 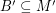 satisfy
satisfy 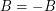 and
and 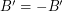 . If there is a homomorphism from
. If there is a homomorphism from 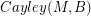 to
to 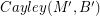 , then every graph with a B-flow has a B'-flow.
, then every graph with a B-flow has a B'-flow.
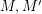 be abelian groups and let
be abelian groups and let 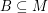 and
and 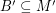 satisfy
satisfy 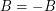 and
and 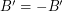 . If there is a homomorphism from
. If there is a homomorphism from 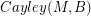 to
to 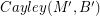 , then every graph with a B-flow has a B'-flow.
, then every graph with a B-flow has a B'-flow. Keywords: homomorphism; nowhere-zero flow; tension
The three 4-flows conjecture ★★
Author(s): DeVos
Conjecture For every graph  with no bridge, there exist three disjoint sets
with no bridge, there exist three disjoint sets 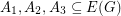 with
with 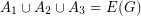 so that
so that 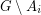 has a nowhere-zero 4-flow for
has a nowhere-zero 4-flow for 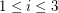 .
.
 with no bridge, there exist three disjoint sets
with no bridge, there exist three disjoint sets 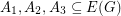 with
with 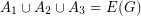 so that
so that 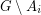 has a nowhere-zero 4-flow for
has a nowhere-zero 4-flow for 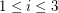 .
. Keywords: nowhere-zero flow
Bouchet's 6-flow conjecture ★★★
Author(s): Bouchet
Conjecture Every bidirected graph with a nowhere-zero  -flow for some
-flow for some  , has a nowhere-zero
, has a nowhere-zero  -flow.
-flow.
 -flow for some
-flow for some  , has a nowhere-zero
, has a nowhere-zero  -flow.
-flow. Keywords: bidirected graph; nowhere-zero flow
Jaeger's modular orientation conjecture ★★★
Author(s): Jaeger
Keywords: nowhere-zero flow; orientation
3-flow conjecture ★★★
Author(s): Tutte
Conjecture Every 4-edge-connected graph has a nowhere-zero 3-flow.
Keywords: nowhere-zero flow

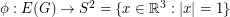 .
.
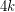 -
-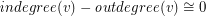 (mod
(mod  ) for every vertex
) for every vertex  .
.  Drupal
Drupal CSI of Charles University
CSI of Charles University