 login/create account
login/create account
Reed's omega, delta, and chi conjecture ★★★
Author(s): Reed
For a graph  , we define
, we define 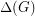 to be the maximum degree,
to be the maximum degree, 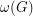 to be the size of the largest clique subgraph, and
to be the size of the largest clique subgraph, and 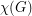 to be the chromatic number of
to be the chromatic number of  .
.
Conjecture 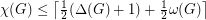 for every graph
for every graph  .
.
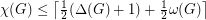 for every graph
for every graph  .
. Keywords: coloring
Seymour's self-minor conjecture ★★★
Author(s): Seymour
Conjecture Every infinite graph is a proper minor of itself.
Keywords: infinite graph; minor
Universal point sets for planar graphs ★★★
Author(s): Mohar
We say that a set 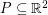 is
is  -universal if every
-universal if every  vertex planar graph can be drawn in the plane so that each vertex maps to a distinct point in
vertex planar graph can be drawn in the plane so that each vertex maps to a distinct point in 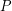 , and all edges are (non-intersecting) straight line segments.
, and all edges are (non-intersecting) straight line segments.
Question Does there exist an  -universal set of size
-universal set of size 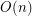 ?
?
 -universal set of size
-universal set of size 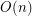 ?
? Keywords: geometric graph; planar graph; universal set

 Drupal
Drupal CSI of Charles University
CSI of Charles University