 login/create account
login/create account
Reed's omega, delta, and chi conjecture
For a graph  , we define
, we define 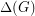 to be the maximum degree,
to be the maximum degree, 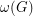 to be the size of the largest clique subgraph, and
to be the size of the largest clique subgraph, and 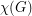 to be the chromatic number of
to be the chromatic number of  .
.
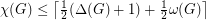 for every graph
for every graph  .
. Perhaps the two most trivial bounds on 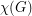 are
are 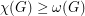 and
and 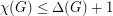 . The above conjecture roughly asserts that the (rounded-up) average of
. The above conjecture roughly asserts that the (rounded-up) average of 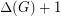 and
and 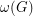 should again be an upper bound on
should again be an upper bound on 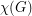 .
.
The conjecture is easy to verify when 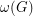 is very large. It is trivial when
is very large. It is trivial when 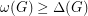 , and it follows from Brook's theorem if
, and it follows from Brook's theorem if 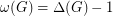 . On the other hand, if
. On the other hand, if 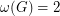 , so
, so  is triangle free, then the conjecture is also true for
is triangle free, then the conjecture is also true for 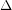 sufficiently large. Indeed, Johannsen proved the much stronger fact that there exists a fixed constant
sufficiently large. Indeed, Johannsen proved the much stronger fact that there exists a fixed constant  so that
so that 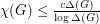 for every triangle free graph
for every triangle free graph  .
.
Reed showed that the conjecture holds when 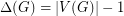 by way of matching theory. More interestingly, he proved (using probabilistc methods) that the conjecture is true provided that
by way of matching theory. More interestingly, he proved (using probabilistc methods) that the conjecture is true provided that 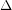 is sufficiently large, and
is sufficiently large, and  is sufficiently close to
is sufficiently close to 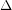 . More precisely, he proves the following:
. More precisely, he proves the following:
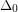 such that for every
such that for every 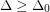 , if
, if  is a graph of maximum degree
is a graph of maximum degree 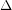 with no clique of size
with no clique of size 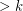 for some
for some 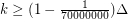 then
then 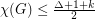 .
. It is known that the conjecture is true fractionally (that is with 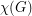 replaced by
replaced by 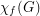 , the fractional chromatic number of~
, the fractional chromatic number of~ ).
).
Bibliography
*[R] B. Reed, 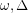 , and
, and 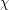 , J. Graph Theory 27 (1998) 177-212.
, J. Graph Theory 27 (1998) 177-212.
* indicates original appearance(s) of problem.
changed
Thanks for the comment. I changed the statement to the conjectured (slightly stronger) version with round-up.

 Drupal
Drupal CSI of Charles University
CSI of Charles University
The statement of the
The statement of the conjecture is slightly incorrect. Instead of the +1 at the end, there should simply be a round-up. The conjecture is true for line graphs and quasi-line graphs, graphs with independence number 2, and any graph on I believe 12 vertices.
An outright proof of the result for triangle-free graphs would be very nice. Lovasz' result on splitting graphs is not quite enough in this case.