 login/create account
login/create account
Multicolour Erdős--Hajnal Conjecture ★★★
Conjecture For every fixed 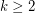 and fixed colouring
and fixed colouring 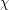 of
of 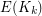 with
with  colours, there exists
colours, there exists 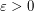 such that every colouring of the edges of
such that every colouring of the edges of 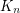 contains either
contains either  vertices whose edges are coloured according to
vertices whose edges are coloured according to 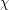 or
or 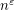 vertices whose edges are coloured with at most
vertices whose edges are coloured with at most 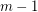 colours.
colours.
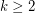 and fixed colouring
and fixed colouring  of
of 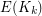 with
with  colours, there exists
colours, there exists 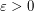 such that every colouring of the edges of
such that every colouring of the edges of 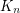 contains either
contains either  vertices whose edges are coloured according to
vertices whose edges are coloured according to 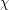 or
or 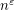 vertices whose edges are coloured with at most
vertices whose edges are coloured with at most 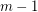 colours.
colours. Keywords: ramsey theory
Sidorenko's Conjecture ★★★
Author(s): Sidorenko
Conjecture For any bipartite graph  and graph
and graph  , the number of homomorphisms from
, the number of homomorphisms from  to
to  is at least
is at least 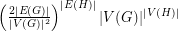 .
.
 and graph
and graph  , the number of homomorphisms from
, the number of homomorphisms from  to
to  is at least
is at least 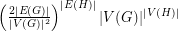 .
. Keywords: density problems; extremal combinatorics; homomorphism
Edge-Unfolding Convex Polyhedra ★★
Author(s): Shephard
Conjecture Every convex polyhedron has a (nonoverlapping) edge unfolding.
Singmaster's conjecture ★★
Author(s): Singmaster
Conjecture There is a finite upper bound on the multiplicities of entries in Pascal's triangle, other than the number 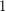 .
.
 .
. The number 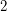 appears once in Pascal's triangle,
appears once in Pascal's triangle, 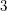 appears twice,
appears twice,  appears three times, and
appears three times, and 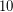 appears
appears 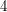 times. There are infinite families of numbers known to appear
times. There are infinite families of numbers known to appear  times. The only number known to appear
times. The only number known to appear 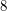 times is
times is 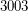 . It is not known whether any number appears more than
. It is not known whether any number appears more than 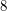 times. The conjectured upper bound could be
times. The conjectured upper bound could be 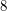 ; Singmaster thought it might be
; Singmaster thought it might be 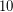 or
or 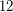 . See Singmaster's conjecture.
. See Singmaster's conjecture.
Keywords: Pascal's triangle

 Drupal
Drupal CSI of Charles University
CSI of Charles University