 login/create account
login/create account
Rainbow AP(4) in an almost equinumerous coloring
Problem Do 4-colorings of 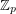 , for
, for 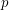 a large prime, always contain a rainbow
a large prime, always contain a rainbow 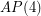 if each of the color classes is of size of either
if each of the color classes is of size of either 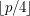 or
or 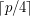 ?
?
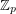 , for
, for 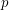 a large prime, always contain a rainbow
a large prime, always contain a rainbow 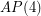 if each of the color classes is of size of either
if each of the color classes is of size of either 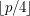 or
or 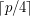 ?
? It is known that there are equinumerous colorings of 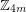 (i.e. colorings of
(i.e. colorings of 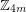 for some
for some  such that each color occurs
such that each color occurs  times) within which we cannot find rainbow arithmetic progressions of length
times) within which we cannot find rainbow arithmetic progressions of length 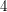 . ([CJR])
. ([CJR])
Bibliography
*[C] David Conlon, Rainbow solutions of linear equations over 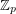 , Discrete Mathematics, 306 (2006) 2056 - 2063.
, Discrete Mathematics, 306 (2006) 2056 - 2063.
[CJR] David Conlon, Veselin Jungic, Rados Radoicic, On the existence of rainbow 4-term arithmetic progressions, Graphs and Combinatorics, 23 (2007), 249-254
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University
Tight hypergraphs
It deservs to be mentioned that in any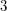 -colouring of
-colouring of 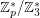 , the equation
, the equation 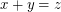 , have an heterochromatic (rainbow) solution; here,
, have an heterochromatic (rainbow) solution; here, 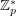 denotes the multiplicative group of the field
denotes the multiplicative group of the field 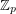 .
.