 login/create account
login/create account
The Double Cap Conjecture
Conjecture The largest measure of a Lebesgue measurable subset of the unit sphere of 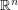 containing no pair of orthogonal vectors is attained by two open caps of geodesic radius
containing no pair of orthogonal vectors is attained by two open caps of geodesic radius 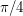 around the north and south poles.
around the north and south poles.
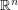 containing no pair of orthogonal vectors is attained by two open caps of geodesic radius
containing no pair of orthogonal vectors is attained by two open caps of geodesic radius 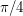 around the north and south poles.
around the north and south poles.
The problem of determining the maximum was first considered by Witsenhausen [Wit] who proved that the measure of such a set is at most 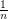 times the surface measure of the sphere. In
times the surface measure of the sphere. In 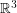 , DeCorte and Pikhurko [DP] improved the multiplicative constant to
, DeCorte and Pikhurko [DP] improved the multiplicative constant to 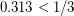 . The conjecture above would imply that the measure is at most
. The conjecture above would imply that the measure is at most 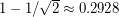 .
.
Bibliography
[DP] E. DeCorte and O. Pikhurko, Spherical sets avoiding a prescribed set of angles, arXiv:1502.05030v2.
[Kalai] G. Kalai, How Large can a Spherical Set Without Two Orthogonal Vectors Be? https://gilkalai.wordpress.com/2009/05/22/how-large-can-a-spherical-set-without-two-orthogonal-vectors-be/
[Wit] H. S. Witsenhausen. Spherical sets without orthogonal point pairs. American Mathematical Monthly, pages 1101–1102, 1974.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University