 login/create account
login/create account
independent set
The Double Cap Conjecture ★★
Author(s): Kalai
Conjecture The largest measure of a Lebesgue measurable subset of the unit sphere of 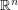 containing no pair of orthogonal vectors is attained by two open caps of geodesic radius
containing no pair of orthogonal vectors is attained by two open caps of geodesic radius 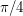 around the north and south poles.
around the north and south poles.
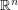 containing no pair of orthogonal vectors is attained by two open caps of geodesic radius
containing no pair of orthogonal vectors is attained by two open caps of geodesic radius 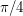 around the north and south poles.
around the north and south poles. Keywords: combinatorial geometry; independent set; orthogonality; projective plane; sphere
Hitting every large maximal clique with a stable set ★★
Conjecture There is a universal constant 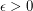 such that every graph contains a stable set which intersects every maximal clique of size
such that every graph contains a stable set which intersects every maximal clique of size 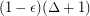 .
.
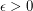 such that every graph contains a stable set which intersects every maximal clique of size
such that every graph contains a stable set which intersects every maximal clique of size 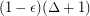 .
.
Conjecture Every graph contains a stable set which intersects every maximal clique of size 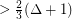 .
.
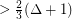 .
. Keywords: independent set; maximal clique
Aharoni-Berger conjecture ★★★
Conjecture If 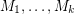 are matroids on
are matroids on 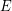 and
and 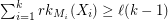 for every partition
for every partition  of
of 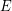 , then there exists
, then there exists 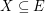 with
with 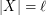 which is independent in every
which is independent in every 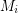 .
.
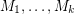 are matroids on
are matroids on 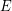 and
and 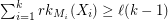 for every partition
for every partition  of
of 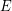 , then there exists
, then there exists 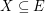 with
with 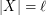 which is independent in every
which is independent in every 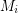 .
. Keywords: independent set; matroid; partition

 Drupal
Drupal CSI of Charles University
CSI of Charles University